Лекция №27. Резонанс токов

Цель: выдать материал про резонанс и условия его возникновения.

Задача: научить определять параметры резонанса.

Резонанс токов может возникать в цепях с параллельным соединением участков, содержащих индуктивности и емкости. Примеры таких цепей приведены на рис. 6.8.

а) б)

Рис. 6.8

Общее условие возникновения резонанса токов– равенство нулю входной реактивной проводимости цепи.

Определим условие возникновения резонанса в цепи с параллельным соединением r, L, c (рис. 6.9).

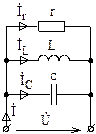
Рис. 6.9

Входная комплексная проводимость цепи

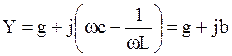. (6.11)

В режиме резонанса входная реактивная проводимость равна нулю ( 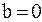) и, следовательно,

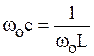. (6.12)

Полученное выражение представляет собой условие возникновения резонанса токов в цепи рис. 6.9.

Частотные характеристики участка L, c (для цепи рис. 6.9) приведены на рис. 6.10.

Рис. 6.10

В области частот ниже резонансной ( 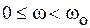) цепь имеет активно-индуктивный характер, а в области выше резонансной ( 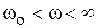) – активно-емкостный.

Из формулы (6.12) следует, что резонанса можно достичь, изменяя частоту входного напряжения, величину индуктивности или емкости:

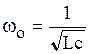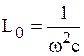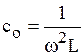, , . (6.13)

В режиме резонанса входная комплексная проводимость цепи (рис. 6.9) 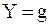и входной ток

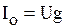(6.14)

минимальны.

Проводимость реактивных элементов на резонансной частоте

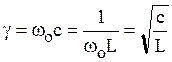(6.15)

называется волновой проводимостью резонансного контура.

Отношение

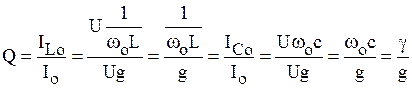(6.16)

называется добротностью резонансного контура.

Добротность показывает, во сколько раз токи реактивных элементов (в режиме резонанса) отличаются от входного тока. Если при резонансе 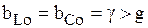и, следовательно, , то токи реактивных элементов (индуктивности и емкости) больше входного тока.

Частотные характеристики (зависимости , ,
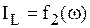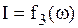) рассматриваемой цепи представлены на рис. 6.11.

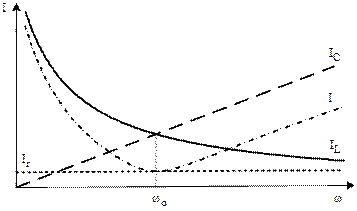
Рис. 6.11

Векторная диаграмма рассматриваемой цепи в режиме резонанса приведена на рис. 6.12.

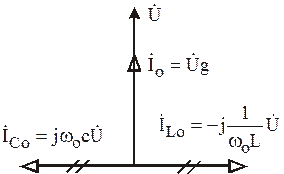
Рис. 6.12

Рассмотрим резонанс токов в цепи с реальной катушкой (рис. 6.13).

Рис. 6.13

Проводимость ветви с индуктивностью

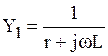. (6.17)

Выделим в комплексной проводимости 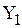действительную и мнимую части, для чего умножим числитель и знаменатель (6.17) на комплексно-сопря­жен­ный знаменатель:

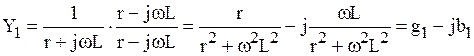. (6.18)

Комплексная проводимость ветви с емкостью

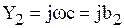. (6.19)

Входная комплексная проводимость цепи

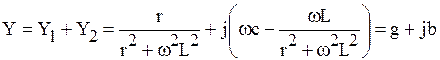. (6.20)

В режиме резонанса входная реактивная проводимость равна нулю ( 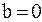) и, следовательно,

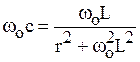. (6.21)

Полученное выражение представляет собой условие возникновения резонанса токов в цепи рис. 6.13. Решая его относительно резонансной частоты 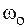, получим

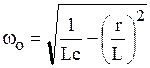. (6.22)

Для построения векторной диаграммы рассматриваемой цепи в режиме резонанса определим токи в параллельных ветвях. Ток в индуктивности

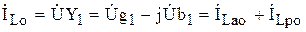, (6.23)

где

(6.24)

– активная составляющая тока в индуктивности;

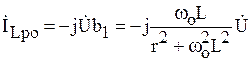(6.25)

– реактивная составляющая тока в индуктивности.

Ток в емкости

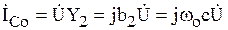. (6.26)

Сопоставление формул (6.21), (6.25) и (6.26) показывает, что

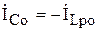. (6.27)

Тогда входной ток цепи в режиме резонанса

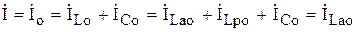. (6.28)

Векторная диаграмма, построенная с учетом (6.27) и (6.28), приведена на рис. 6.14.

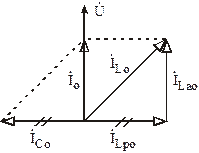
Рис. 6.14