Лекция №23. Последовательное соединение индуктивно-связаных элементов.

Цель: расширить знания студентов по теме индуктивно-связанных элементов

Задача: научить рассчитывать цепи с взаимной индуктивностью.

Две катушки с сопротивлениями R₁ и R₂, индуктивностями L₁ и L₂ и взаимной индуктивностью М соединены последовательно. Возможны два вида их включения: согласное (рис. 4.4а) и встречное (рис. 4.4б).

При согласном включении токи в обоих элементах в любой момент времени направлены одинаково относительно одноименных выводов, поэтому магнитные потоки самоиндукции Ф₁₁ (или Ф₂₂) и взаимной индукции Ф₁₂ (или Ф₂₁), сцепленные с каждым элементом, складываются. При встречном включении токи в обоих элементах цепи в любой момент времени направлены противоположно относительно одноименных выводов, поэтому магнитные потоки самоиндукции и взаимной индукции, сцепленные с каждым элементом, вычитаются.

Индуктивность двух последовательно соединенных индуктивно связанных элементов определяется выражением:

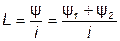, (4.7)

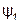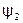где и - потокосцепления первого и второго элементов, причем ; .

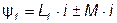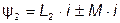Знак плюс относится к согласному, а знак минус ко встречному включению. Следовательно,

L = L₁ + L₂ ± 2M.

Полное сопротивление при согласном включении больше, чем при встречном.

Напряжения на элементах имеют по три составляющие:

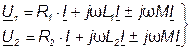(4.8)

Если индуктивность одного из элементов меньше взаимной индуктивности, то при встречном включении наблюдается своеобразный «емкостный» эффект. Пусть, например, L₂ < М, при этом в выражении

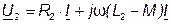
имеем ω(L₂-M) < 0, и, следовательно, напряжение 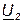отстает по фазе от тока 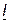, как в случае емкостного сопротивления. Конечно, реактивное сопротивление всей цепи в целом индуктивное, так как L = L₁+ L₂ - 2М > 0 и ток 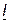отстает по фазе от напряжения .

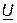На (рис. 4.5а,б) показаны векторные диаграммы для согласного и встречного включений при одинаковом значении тока в обоих случаях.

Входное комплексное сопротивление цепи получаем, учитывая (4.8)

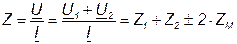; (4.9)

где 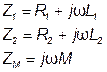(4.10)