Топографическая векторная диаграмма

Частным случаем векторной диаграммы является топографическая векторная диаграмма, на которой откладываются комплексные потенциалы отдельных точек цепи по отношению к одной точке, потенциал которой принят равным нулю. Порядок расположения векторов на топографической диаграмме соответствует порядку расположения элементов цепи.

Отметим, что по определению топографическая диаграмма используется как геометрическая интерпретация второго закона Кирхгофа (т.е. на ней откладываются векторы напряжений).

Существуют два способа построения топографической диаграммы.

I способ.

Строят, двигаясь по элементам цепи в направлении, совпадающем с направлением тока. В этом случае вектор напряжения на диаграмме и соответствующая стрелка напряжения на схеме ориентированы одинаково – от высшего потенциала к низшему.

Рассмотрим в качестве примера цепь рис. 3.15.

Рис. 3.15

Отложим на комплексной плоскости вектор тока 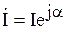под углом 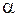к действительной оси (рис. 3.16).

Рис. 3.16

Обозначим промежуточные точки рассматриваемой цепи буквами a, b, d, h. Обход контура будем совершать по направлению тока (т. е. по часовой стрелке), принимая комплексный потенциал точки а равным нулю. Последнее приводит к тому, что на комплексной плоскости точка а расположена в начале координат (рис. 3.16).

При движении в выбранном направлении по элементам цепи из точки а (рис. 3.15) первым элементом цепи является емкость с. Откладываем на топографической диаграмме из точки а вектор напряжения на емкости 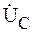, который отстает от тока на угол 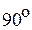(рис. 3.17). Конец вектора 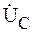определяет величину комплексного потенциала точки b на векторной диаграмме.

Следующий элемент цепи при движении по направлению тока – сопротивление r (см. рис. 3.15). Откладываем на топографической диаграмме вектор напря­жения на сопротивлении 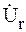, который совпадает по направлению с вектором тока 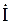(рис. 3.18).

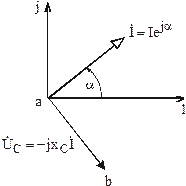
Рис. 3.17

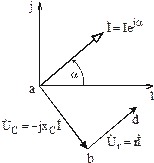
Рис. 3.18

Конец вектора 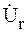определяет величину комплексного потенциала точки d на векторной диаграмме.

Следующий элемент цепи при движении по направлению тока – индуктивность L (см. рис. 3.15). Откладываем на топографической диаграмме вектор напряжения на индуктивности 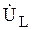, который опережает вектор тока 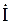(рис. 3.19). Конец вектора 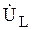определяет величину комплексного потенциала точки h на векторной диаграмме.

Разность потенциалов точек a и h равна входному напряжению цепи 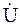(см. рис. 3.15). Для получения соответствующего вектора на диаграмме необходимо соединить прямой линией точки a и h. Конец вектора 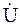на диаграмме должен быть направлен так же, как и стрелка напряжения на схеме, – от точки а к точке h (рис. 3.20).

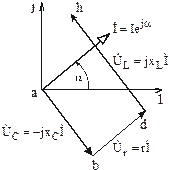
Рис. 3.19

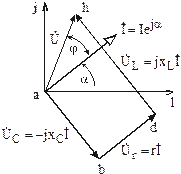
Рис. 3.20

Угол между векторами напряжения и тока (рис. 3.20) равен углу сдвига фаз 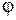. В данном случае входное напряжение опережает ток и цепь имеет активно-индуктивный характер.

2 способ.

Строят, двигаясь по элементам цепи в направлении, противоположном направлению тока. В этом случае вектор напряжения на диаграмме направлен от точки низшего потенциала к точке высшего потенциала. Это же напряжение на схеме указывается стрелкой противоположного направления.

Итак, будем совершать обход цепи рис. 3.21 в направлении, противоположном току, принимая комплексный потенциал точки h равным нулю.

Рис. 3.21

Последнее приводит к тому, что на комплексной плоскости точка h расположена в начале координат (рис. 3.22).

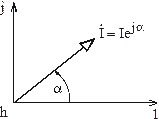
Рис. 3.22

При движении в выбранном направлении по элементам цепи из точки h (рис. 3.21) первым элементом цепи является индуктивность L. Откладываем на топографической диаграмме из точки h вектор напряжения на индуктивности 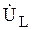, который опережает вектор тока 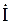(рис. 3.23). Конец вектора 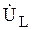определяет величину комплексного потенциала точки d на векторной диаграмме.

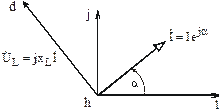
Рис. 3.23

Продолжая движение в выбранном направлении по элементам цепи и осуществляя аналогичные построения, получим результирующую топографическую диаграмму рис. 3.24.

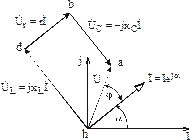
Рис. 3.24

Сравнение векторных диаграмм рис. 3.20 и 3.24, построенных двумя способами, показывает их полную идентичность (векторы одноименных величин на диаграммах имеют одинаковое направление). Область преимущественного использования второго способа – трехфазные цепи.