Векторная диаграмма ЛЕП 110 кВ с одной нагрузкой
При построении векторной диаграммы примем допущение, что потери мощности на корону в сети отсутствуют. В этом случае схема замещения ЛЭП представлена П-образной схемой: активным R и реактивным X сопротивлениями и емкостной проводимостью B/2 в начале и конце ЛЭП (см. рис. 8.5). В них протекают токи 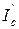 и
и 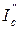 . В сопротивлениях ЛЭП протекает ток IZ. Нужно определить U1ф, I1 и cos φ1.
. В сопротивлениях ЛЭП протекает ток IZ. Нужно определить U1ф, I1 и cos φ1.
 Ток IZ представляет собой геометрическую сумму тока нагрузки и тока проводимости в конце ЛЕП:
Ток IZ представляет собой геометрическую сумму тока нагрузки и тока проводимости в конце ЛЕП:
IZ = I2 + 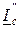 .
.
Ток в проводимости опережает напряжение в конце ЛЭП на 900 и рассчитывается по формуле:
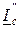 = U2ф· B/2.
= U2ф· B/2.
Напряжение в начале ЛЕП отличается от напряжения в конце на величину падения напряжения в сопротивлениях и проводимостях ЛЭП:
U1ф = U2ф + ΔUф.
Падение напряжения рассчитывается следующим образом:
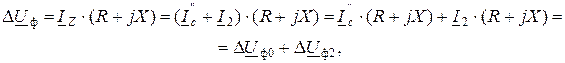
т.е. полное падение напряжение в нагруженной ЛЭП складывается из падения напряжения при холостом ходе U0ф, вызванного током 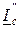 , и падения напряжения ΔUф2, вызванного током нагрузки I2.
, и падения напряжения ΔUф2, вызванного током нагрузки I2.
Построение векторной диаграммы начнем с построения вектора падения напряжения от тока проводимости. По действительной оси откладывем напря-жение U2ф (см. рис. 8.6). Получаем точку а. Под углом 900 откладываем опережающий ток 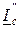 .
.
 |
От конца вектора U2ф параллельно линии тока
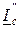 откладываем вектор падения напряжения в активном сопротивлении ЛЭП. Получаем точку b. Под углом 900 к нему в сторону опережения откладываем вектор падения напряжения в реактивном сопротивлении. Получаем точку c. Соединяем начало координат с точкой c и получаем напряжение в начале ЛЭП в режиме холостого хода U1ф0.
откладываем вектор падения напряжения в активном сопротивлении ЛЭП. Получаем точку b. Под углом 900 к нему в сторону опережения откладываем вектор падения напряжения в реактивном сопротивлении. Получаем точку c. Соединяем начало координат с точкой c и получаем напряжение в начале ЛЭП в режиме холостого хода U1ф0.
Стороны треугольника падения напряжения от тока холостого хода (тока 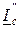 ) пропорциональны:
) пропорциональны:
ab≡ 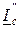 ∙R; bc≡
∙R; bc≡ 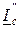 ∙X; ac≡
∙X; ac≡ 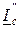 ∙Z.
∙Z.
Под углом φ2 к напряжению U2ф откладываем ток I2. От точки с параллельно линии тока I2 откладываем вектор падения напряжения в активном сопротивлении ЛЭП. Получаем точку d. Под углом 900 к нему в сторону опережения откладываем вектор падения напряжения в реактивном сопротивлении. Получаем точку e. Соединяем начало координат с точкой e и получаем напряжение в начале ЛЭП U1ф.
Стороны треугольника падения напряжения от тока нагрузки (тока I2) пропорциональны:
cd≡ I2∙R; de≡ I2∙X; ce≡ I2∙Z.
Если соединить точку а с точкой е, получим вектор полного падения напряжения от тока IZ протекающего в ЛЭП. Его проекции на действительную и мнимую оси дают продольную и поперечную составляющие падения напряжения:
∆Uф ≡ af ; δUф ≡ ef .
На диаграмме видно, что величина тока IZ меньше тока нагрузки. Это объясняется тем, что емкостный ток проводимости в конце ЛЭП, протекая по линии совместно с током нагрузки, компенсирует соответствующую величину индуктивной составляющей тока нагрузки.
Чтобы определить ток I1 в начале ЛЭП, необходимо сложить векторы IZ и 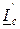 :
:
I1 = IZ + 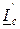 .
.
Вектор тока 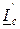 в проводимости в начале ЛЭП опережает напряжение U1ф на 900. Угол между напряжением U1ф и током I1 обозначим φ1.
в проводимости в начале ЛЭП опережает напряжение U1ф на 900. Угол между напряжением U1ф и током I1 обозначим φ1.
Определим из диаграммы значения векторов ∆Uф и δUф. Спроецируем векторы 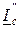 ∙R,
∙R, 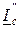 ∙X, I2∙R и I2∙X на обе оси. Получим точки с’, b’, d’ и f ’. Отрезок dd’ продолжим до пересечения с отрезком bb’. Получим точку k. Рассмотрим два треугольника - ckd и def ‘. Эти треугольники подобны по двум углам:
∙X, I2∙R и I2∙X на обе оси. Получим точки с’, b’, d’ и f ’. Отрезок dd’ продолжим до пересечения с отрезком bb’. Получим точку k. Рассмотрим два треугольника - ckd и def ‘. Эти треугольники подобны по двум углам: 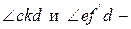 прямые;
прямые; 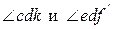 дополняют
дополняют 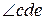 до прямого угла.
до прямого угла.
Из треугольников получим:
c’d’ = ck = I2∙R· cos φ2; dk = b’f ‘ = I2∙R sin φ2;
fd’ = d’f = I2∙X· sin φ2; ef ‘ = I2∙X cos φ2.
Величина продольной составляющей падения напряжения рассчитывается следующим образом:
∆Uф = c’d’ + fd’ – c’a = I2∙R· cos φ2 + I2∙X· sin φ2 – 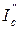 ∙X.
∙X.
Величина поперечной составляющей падения напряжения определяется из выражения:
δUф = ef ‘ – ff ‘ = ef ‘ – (b’f ‘ – bf ‘) = ef ‘ – b’f ‘ + bf ‘ = I2∙X cos φ2 – I2∙R sin φ2 + 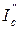 ∙R.
∙R.
Найдем формулы для расчета величины линейных значений ∆U и δU. Для этого полученные выражения умножим на множитель 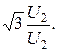 В результате преобразований, получим:
В результате преобразований, получим:
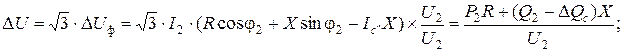
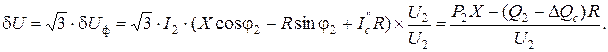
Из приведенных выражений следует, что зарядные мощности ЛЭП уменьшают продольную составляющую падения напряжения (потерю напряжения) и увеличивают поперечную составляющую.
Это можно показать и на векторной диаграмме. При учете тока 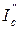 в проводимости величина потери напряжения уменьшается на величину отрезка аc’, а поперечная составляющая падения напряжения увеличивается на величину отрезка b’f. Следствием этого является увеличение сдвига фаз между напряжениями U1ф и U2ф.
в проводимости величина потери напряжения уменьшается на величину отрезка аc’, а поперечная составляющая падения напряжения увеличивается на величину отрезка b’f. Следствием этого является увеличение сдвига фаз между напряжениями U1ф и U2ф.
Уменьшение потери напряжения благоприятно сказывается на режиме работы ЛЭП, особенно при больших и средних нагрузках. При некоторой небольшой нагрузке линии потеря напряжения, вызванная током нагрузки I2, будет полностью скомпенсирована отрицательной потерей напряжения от емкостного тока проводимости 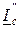 . В этом случае передача мощности будет выполняться при равенстве напряжений в начале и конце ЛЭП. При дальнейшем снижении тока нагрузки отрицательная потеря напряжения от тока
. В этом случае передача мощности будет выполняться при равенстве напряжений в начале и конце ЛЭП. При дальнейшем снижении тока нагрузки отрицательная потеря напряжения от тока 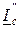 станет больше потери напряжения от тока нагрузки. Напряжение в начале ЛЭП станет меньше напряжения в конце (см. векторную диаграмму при холостом ходе). Такой режим недопустим. Мощность, генерируемая емкостями ЛЭП, направлена в сторону генераторов и будет оказывать подмагничивающее действие на их магнитную систему. В результате будет увеличиваться напряжения на шинах генераторов и в сети, которая питается от этих шин. В сетях с глухозаземленной нейтралью в режиме холостого хода напряжение в сети может превысить величину напряжения, на которую рассчитана изоляция оборудования.
станет больше потери напряжения от тока нагрузки. Напряжение в начале ЛЭП станет меньше напряжения в конце (см. векторную диаграмму при холостом ходе). Такой режим недопустим. Мощность, генерируемая емкостями ЛЭП, направлена в сторону генераторов и будет оказывать подмагничивающее действие на их магнитную систему. В результате будет увеличиваться напряжения на шинах генераторов и в сети, которая питается от этих шин. В сетях с глухозаземленной нейтралью в режиме холостого хода напряжение в сети может превысить величину напряжения, на которую рассчитана изоляция оборудования.
Лекция № 9
Расчет режимов электрических сетей
План.
1. Задача расчета режимов. Основные допущения.
2. Расчет режима при заданном напряжении в конце ЛЭП.
3. Расчет режима при заданном напряжении в начале ЛЭП (на источнике питания).
4. Расчет сетей разных номинальных напряжений.
Дата добавления: 2015-02-13; просмотров: 1824;
