Векторная алгебра. Аналитическая геометрия в пространстве.

61–70. Убедиться, что векторы 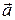, , 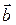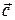не лежат в одной плоскости, написать разложение вектора 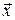по векторам , , .

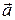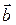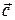61. 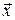={15; –20; –1}, 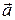={0; 2; 1}, 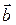={0; 1; –1}, 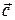={5; –3; 2}.

62. 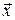={2; 7; 5}, 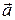={1; 0; 1}, 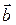={1; –2; 0}, 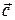={0; 3; 1}.

63. 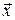={8; –7; –13}, 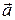={0; 1; 5}, 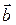={3; –1; 2}, 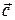={–1; 0; 1}

64. 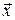={0; –8; 9}, 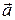={0; –2; 1}, 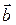={3; 1; –1}, 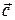={4; 0; 1}.

65. 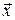={ –13; 2; 18}, 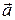={1; 1; 4}, 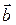={–3; 0; 2}, 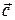={1; 2; –1}.

66. 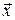={11; –1; 4}, 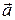={1; –1; 2}, 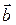={3; 2; 0}, 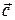={–1; 1; 1}.

67. 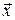={–1; 7; 0}, 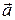={0; 3; 1}, 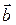={1; –1; 2}, 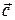={2; –1; 0}.

68. 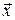={3; 1; 3}, 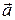={2; 1; 0}, 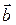={1; 0; 1}, 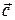={4; 2; 1}.

69. 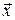={23; –14; –30}, 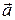={2; 1; 0}, 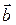={1; –1; 0}, 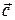={–3; 2; 5}.

70. 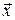= {8; 9; 4}, 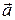= {1; 0; 1}, 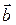={0; –2; 1}, 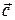={1; 3; 0}.

71–80.Точки А_1, А_2, А_3, А₄ являются вершинами пирамиды. Вычислить: 1) длину ребра А₁А₂; 2) угол между ребрами А₁А₂ и А₃А₂;3) площадь грани А₁А₂А₃; 4) объем пирамиды; 5) уравнение прямой А₁А₃; 6) уравнение плоскости А₂А₃А₄; 7) уравнение высоты, опущенной из вершины А₁ на грань А₂А₃А₄; 8) длину этой высоты. Сделать чертеж.

71. А₁(1;–1; 2), А₂(2; 1; 2), А₃(1; 1; 4), А₄(6;–3; 8).

72. А₁(2;–4;–3), А₂(5;–6; 0), А₃(–1; 3;–3), А₄(–10;–8; 7).

73. А₁(–3;–5; 6), А₂(2; 1;–4), А₃(0;–3;–1), А₄(–5; 2;–8).

74. А₁(–2;–1;–1), А₂(0; 3; 2), А₃(3; 1;–4), А₄(–4; 7; 3).

75. А₁(1; 3; 0), А₂(4;–1; 2), А₃(3; 0; 1), А₄(–4; 3; 5).

76. А₁(0;–3; 1), А₂(–4; 1; 2), А₃(2;–1; 5), А₄(3; 1;–4).

77. А₁(–1; 2; 4), А₂(–1;–2;–4), А₃(3; 0;–1), А₄(7;–3; 1).

78. А₁(3; 10;–1), А₂(–2; 3;–5), А₃(–6; 0;–3), А₄(1;–1; 2).

79. А₁(1; 2;–3), А₂(1; 0; 1), А₃(–2;–1; 6), А₄(0;–5;–4).

80. А₁(1; 0; 2), А₂(1; 2;–1), А₃(2;–2; 1), А₄(2; 1; 0).