Разложение вектора по базису.
Любые три вектора 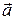 ,
, 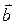 ,
, 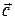 , не лежащие в одной плоскости, могут быть приняты за базис в
, не лежащие в одной плоскости, могут быть приняты за базис в 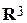 . Всякий вектор
. Всякий вектор 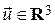 может быть разложен по этому базису, т. е. представлен в виде
может быть разложен по этому базису, т. е. представлен в виде 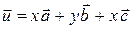 .
.
Пример. Найти объем параллелепипеда, построенного на векторах
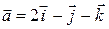 ;
; 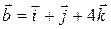 ,
, 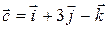 .
.
Решение. Найдем смешанное произведение
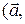
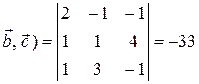 ,
,
Объем 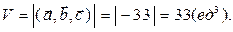
Пример. Убедиться, что векторы 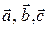 не лежат в одной плоскости, написать разложение вектора
не лежат в одной плоскости, написать разложение вектора 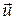 по векторам
по векторам 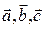 если
если
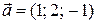 ;
; 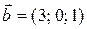 ;
; 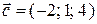 ;
; 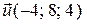 .
.
Решение. 1) Проверяем условие компланарности для векторов 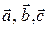 .
.

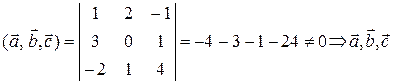 не лежат в одной плоскости и могут быть приняты за базис.
не лежат в одной плоскости и могут быть приняты за базис.
2) Разложим вектор 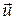 по векторам
по векторам 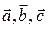 :
:
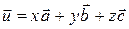 .
.
Чтобы найти 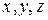 запишем это равенство для каждой координаты
запишем это равенство для каждой координаты
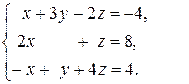
Решив систему уравнений любым известным способом, находим 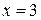 ;
; 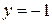 ;
; 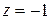 . Значит,
. Значит, 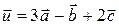 .
.
Дата добавления: 2015-01-29; просмотров: 1511;
