Лекция 27. Сингулярное разложение матрицы

Необходимо отметить, что QR, QL-алгоритмы в общем случае сохраняют ширину ленты исходной матрицы. Для определенности рассмотрим далее QR-алгоритм. Пусть для ненулевой ленточной -матрицы построено QR-разложение:

где 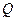— ортогональная матрица с элементами ;

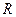— верхняя треугольная матрица с элементами .

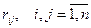Пусть 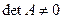. Рассмотрим значения элементов последней строки матрицы :

, (7.3)

откуда вытекает, что .

Составляя уравнение, аналогичное (7.3) для , получим из него, что .

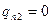Первый ненулевой элемент в последней строке матрицы 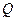будет находится в той же позиции, что и первый ненулевой элемент в последней строке матрицы . Рассмотрев последовательно выражения для значений всех элементов , двигаясь по строкам снизу вверх, получим, что структура нижнего треугольника матрицы 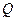аналогична ленточной структуре нижнего треугольника матрицы :

На очередной итерации основного QR-алгоритма (без использования сдвигов для ускорения сходимости) получаем матрицу

. (7.4)

Таким образом, если исходная матрица была симметричной, то итерации QR-алгоритма сохраняют симметричность:

. (7.5)

Сохранение нулевих элементов (ленточной структуры) в нижнем треугольнике матрицы вытекает из вида 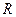и :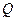

Действительно, при вычислении элементов последней строки матрицы получаем, что первым отличным от нуля может быть лишь элемент, стоящий на том же месте, что и первый отличный от нуля элемент последней строки матрицы :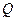

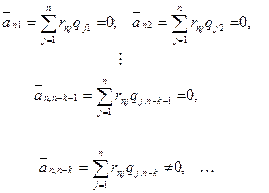
Аналогичный результат в нижнем треугольнике получится и при вычислении элементов всех строк матрицы .

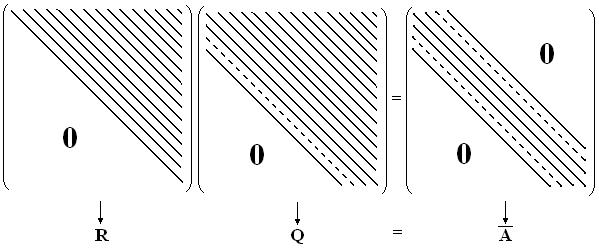
Сохранение исходной ленточной структуры матрицы в верхнем треугольнике матрицы вытекает из (7.5). Таким образом, соотношение (7.6) можно уточнить:

Замечание.Поскольку QR-алгоритм сохраняет ширину ленты матрицы, не имеет смысла приводить ленточную матрицу к трехдиагональному виду на подготовительном этапе, поскольку накладные вычислительные расходы такого приведения могут оказаться значительно превосходящими вычислительные расходы самого QR-алгоритма при работе с имеющейся ленточной матрицей.

Лекция 27. Сингулярное разложение матрицы