Теорема о сингулярном разложении матрицы
Пусть 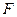 —
— 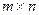 -матрица с элементами
-матрица с элементами 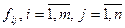 , (
, ( 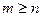 ). Для нее справедливо разложение, называемое сингулярным:
). Для нее справедливо разложение, называемое сингулярным:
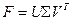 ,(1)
,(1)
где 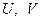 ― матрицы размерности
― матрицы размерности 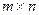 и
и 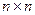 соответственно,
соответственно, 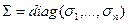 ,
, 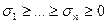 , при этом
, при этом 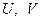 являются ортогональными , т.е. удовлетворяют соотношениям:
являются ортогональными , т.е. удовлетворяют соотношениям: 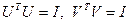 , где
, где 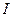 ― единичная матрица соответствующей размерности. Столбцы
― единичная матрица соответствующей размерности. Столбцы 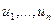 матрицы
матрицы 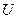 и
и 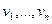 матрицы
матрицы 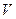 называют соответственно левыми и правыми сингулярными векторами (СНВ) матрицы
называют соответственно левыми и правыми сингулярными векторами (СНВ) матрицы 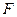 , величины
, величины 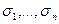 ― сингулярными числами (СНЧ), а
― сингулярными числами (СНЧ), а 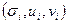 сингулярными тройками
сингулярными тройками 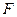 . При
. При 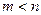 рассматривается сингулярное разложение матрицы
рассматривается сингулярное разложение матрицы 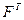 .
.
Разложение (1) может быть представленно в форме внешних произведений:
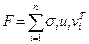 .
.
В общем случае сингулярное (спектральное) разложение матрицы определяется неоднозначно. Вспомним, что вектор 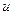 называется лексикографически положительным, если его первая ненулевая компонента положительна. Назовем сингулярное разложение (1) нормальным, если столбцы матрицы
называется лексикографически положительным, если его первая ненулевая компонента положительна. Назовем сингулярное разложение (1) нормальным, если столбцы матрицы 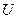 лексикографически положительны.
лексикографически положительны.
Теорема.Невырожденная матрица 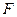 имеет единственное нормальное сингулярное разложение, если ее СНЧ попарно различны:
имеет единственное нормальное сингулярное разложение, если ее СНЧ попарно различны:
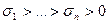 .
.
Дата добавления: 2015-03-20; просмотров: 1327;
