Чувствительность собственных значений (сингулярных чисел) и собственных векторов (сингулярных векторов) к возмущающим воздействиям

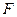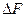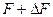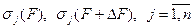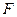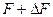Пусть исходная матрица претерпела возмущение , в результате которого получена матрица . Для СНЧ , матриц и соответственно имеет место соотношение:

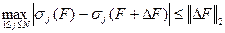, (8)

где 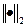― спектральная матричная норма.

В силу соотношения (8) возмущения СНЧ сравнимы с возмущением данных ― 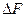, т.е. СНЧ матрицы являются нечувствительными к возмущающим воздействиям.

Для СЗ симметричной матрицы 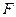имеет место аналогичная оценка:

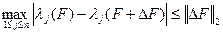. (9)

В силу соотношения (9) возмущения СЗ, как и СНЧ в соответствии с (8), сравнимы с возмущением данных ― 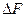, СЗ симметричной матрицы являются нечувствительными к возмущающим воздействиям, или хорошо обусловленными.

Чувствительность СВ 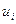, отвечающего СЗ 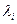, в пределах матрицы 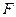определяется в соответствии с соотношениями

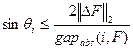, (10)

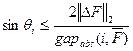, (11)

где 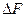— возмущение матрицы 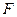, , 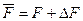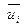— нормированный возмущенный СВ,

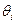— острый угол между 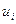и ,

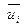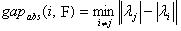(12)

— абсолютная отделенность СЗ 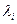матрицы .

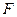Утверждение.Абсолютная отделенность СЗ матрицы является мерой чувствительности соответствующего СВ к возмущающим воздействиям.

Аналогично тому, как это было сделано в случае симметричной матрицы в соотношении (12), назовем отделенностью СНЧ 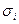матрицы 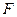величину

.

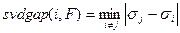Пусть 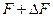— возмущенная матрица, 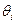— угол между соответствующими исходным и возмущенным сингулярными векторам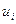и и 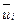, тогда имеют место соотношения, аналогичные (10), (11):

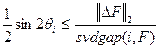при условии ,

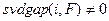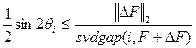при условии .

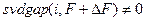Таким образом, реакция СВ (СНВ) матрицы на возмущающее воздействие будет разной, она будет зависеть от значения абсолютной отделенности (отделенности) соответствующего собственного значения (СНЧ): чем больше абсолютная отделенность (отделенность) СЗ (СНЧ), тем менее чувствительным к возмущающим воздействиям будет соответствующий СВ (СНВ).