Комплексные числа
4.1.Комплексным числом называется выражение вида:
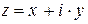 ,
,
где 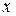 и
и 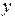 — любые действительные числа, а
— любые действительные числа, а 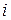 — так называемая мнимая единица, удовлетворяющая условию
— так называемая мнимая единица, удовлетворяющая условию
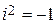 .
.
Числа 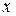 и
и 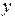 называются соответственно действительной и мнимой частями комплексного числа
называются соответственно действительной и мнимой частями комплексного числа 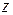 .
.
Комплексные числа можно представлять точками  плоскости
плоскости  или же векторами
или же векторами  этой плоскости.
этой плоскости.
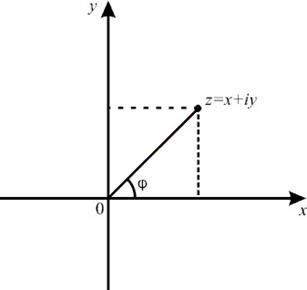
4. 2. Длина 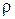 вектора
вектора 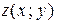 называется модулем комплексного числа и обозначается через
называется модулем комплексного числа и обозначается через 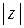 , так что
, так что 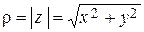 .
.
Угол 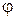 , образованный вектором
, образованный вектором 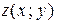 с положительным направлением оси
с положительным направлением оси 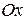 называется аргументом комплексного числа
называется аргументом комплексного числа 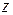 и обозначается
и обозначается
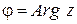 .
.
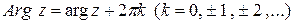 ,
,
где 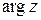 – главное значение
– главное значение 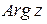 , определяемое условиями
, определяемое условиями 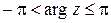 , причем,
, причем,
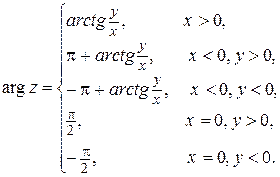
Так как 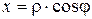 ,
, 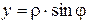 , то
, то  — тригонометрическая форма комплексного числа. С помощью формулы Эйлера
— тригонометрическая форма комплексного числа. С помощью формулы Эйлера
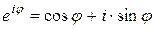
можно перейти от тригонометрической формы к показательной
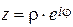 .
.
4. 3. Два комплексных числа 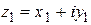 и
и 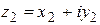 равны тогда и только тогда, когда равны их вещественные и мнимые части:
равны тогда и только тогда, когда равны их вещественные и мнимые части: 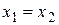 ;
; 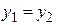 . Или когда их модули равны, а аргументы либо равны, либо отличаются на величину, кратную
. Или когда их модули равны, а аргументы либо равны, либо отличаются на величину, кратную 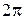 :
:
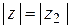 ,
, 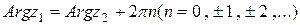
4. 4. Основные действия над комплексными числами.
При сложении и вычитании комплексных чисел отдельно складываются или вычитаются их действительные и мнимые части
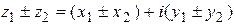 .
.
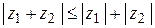 ,
, 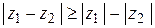 .
.
Умножение: 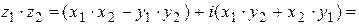
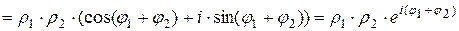 .
.
Деление:
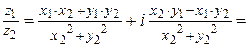
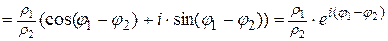 .
.
Возведение в степень 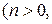 целое):
целое):
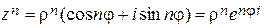 .
.
Корень из комплексного числа 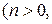 целое):
целое):
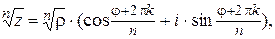
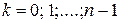 .
.
Корень 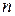 – ой степени из любого числа
– ой степени из любого числа 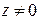 имеет
имеет 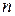 различных значений, которые располагаются в вершинах правильного
различных значений, которые располагаются в вершинах правильного 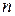 – угольника, вписанного в окружность радиуса
– угольника, вписанного в окружность радиуса 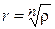 с центром в начале координат.
с центром в начале координат.
Пример. Даны комплексные числа в алгебраической форме:
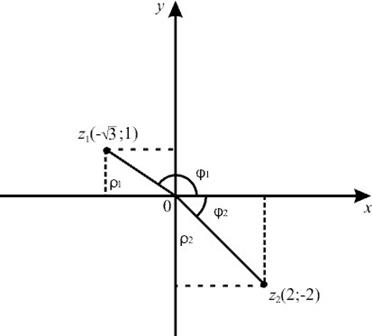
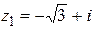 ;
; 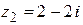 . Записать их в тригонометрической и показательной формах, изобразить на комплексной плоскости.
. Записать их в тригонометрической и показательной формах, изобразить на комплексной плоскости.
Выполнить указанные действия: 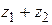 ,
, 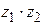 ,
, 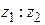 ,
, 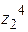 . Найти все корни уравнения
. Найти все корни уравнения 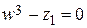 , изобразить их на плоскости.
, изобразить их на плоскости.
Решение.
Изобразим числа 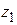 и
и 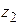 на комплексной плоскости
на комплексной плоскости
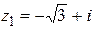 ,
, 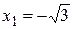 ,
, 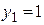 .
.
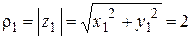 ,
,
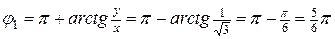 .
.
Тригонометрическая форма:
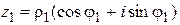 ,
, 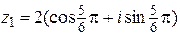 .
.
Показательная форма числа: 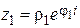 ;
; 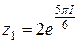 .
.
Для 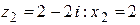 ;
; 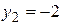 ;
; 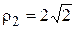 ;
; 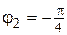
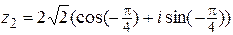 ,
, 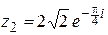
Выполним действия:
1) 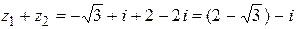 ,
,
2) 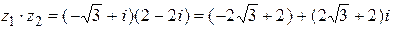 ,
,
Умножаем по правилу умножения многочленов, учитывая, что 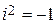 или
или 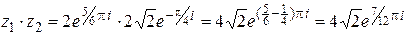 . (При умножении показатели складываются).
. (При умножении показатели складываются).
3) 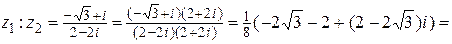
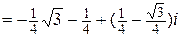 .
.
В показательной форме:
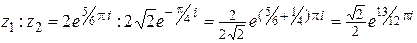 . (При делении показатели вычитаются).
. (При делении показатели вычитаются).
4) 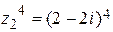 . Лучше это действие выполнять в показательной форме
. Лучше это действие выполнять в показательной форме 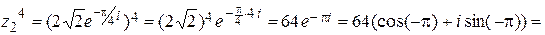
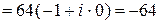 .
.
Найдем корни уравнения 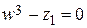 ,
, 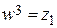 .
.
Корень третьей степени из комплексного числа имеет три различные значения. В данном случае
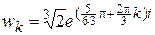 .
.
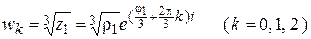
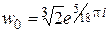 ,
, 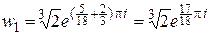 ,
,
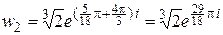
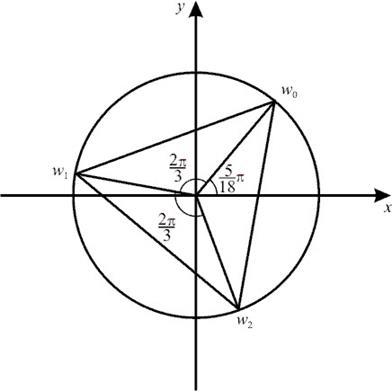
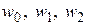 имеют одинаковый модуль, значит они располагаются на окружности с центром в начале координат, радиусом
имеют одинаковый модуль, значит они располагаются на окружности с центром в начале координат, радиусом 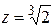 , так как разность аргументов
, так как разность аргументов 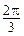 , то они лежат в вершинах правильного вписанного треугольника.
, то они лежат в вершинах правильного вписанного треугольника.
Задания по теме «Элементы линейной алгебры»
1-10. Вычислить матрицу 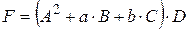 , если
, если
1. 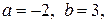
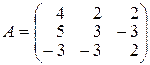 ,
, 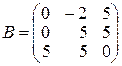 ,
, 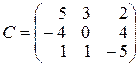 ,
, 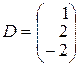 .
.
2. 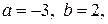
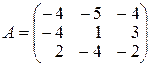 ,
, 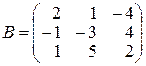 ,
, 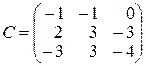 ,
, 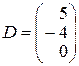 .
.
3. 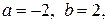
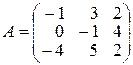 ,
, 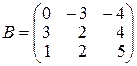 ,
, 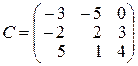 ,
, 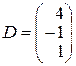 .
.
4. 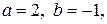
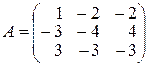 ,
, 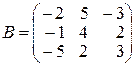 ,
, 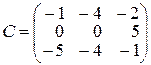 ,
, 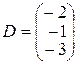 .
.
5. 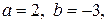
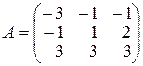 ,
, 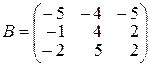 ,
, 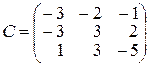 ,
, 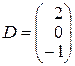 .
.
6. 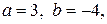
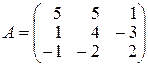 ,
, 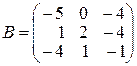 ,
, 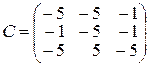 ,
, 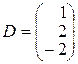 .
.
7. 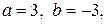
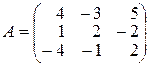 ,
, 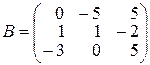 ,
, 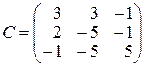 ,
, 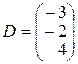 .
.
8. 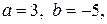
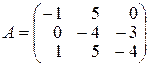 ,
, 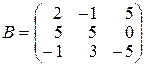 ,
, 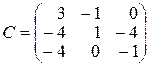 ,
, 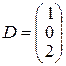 .
.
9. 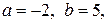
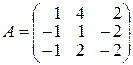 ,
, 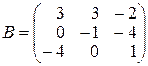 ,
, 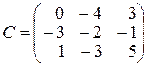 ,
, 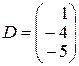 .
.
10. 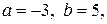
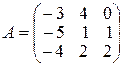 ,
, 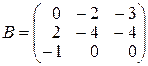 ,
, 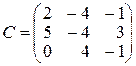 ,
, 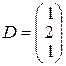 .
.
11-20. Найти обратную для матрицы А, проверить, что А-1А=Е:
11. 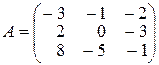 .
.
12. 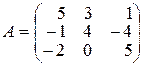 .
.
13. 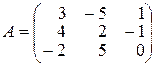 .
.
14. 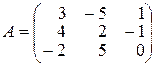 .
.
15. 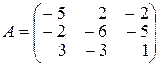 .
.
16. 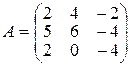 .
.
17. 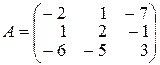 .
.
18. 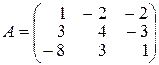 .
.
19. 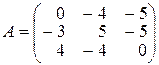 .
.
20. 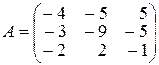
21-30. Найти решение системы линейных уравнений: а) по формулам Крамера и с помощью обратной матрицы;
21. а) 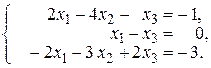 б)
б)
22. а) 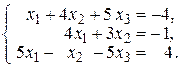 б)
б)
23. а) 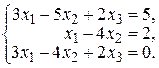 б)
б)
24. а) 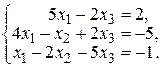 б)
б)
25. а) 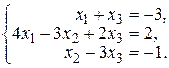 б)
б)
26. а) 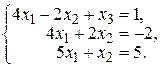 б)
б)
27. а) 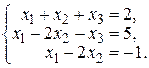 б)
б)
28. а) 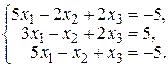 б)
б)
29. а) 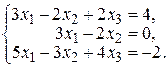 б)
б)
30. а) 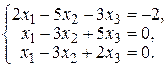 б)
б)
Дата добавления: 2015-01-29; просмотров: 1519;
