Основные действия с векторами.
Пусть 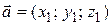 ,
, 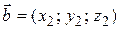 ,
, 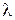 – скаляр.
– скаляр.
1°. 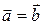 Û
Û 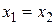 ,
, 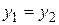 ,
, 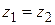 .
.
2°. 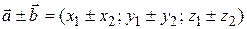 .
.
3°. 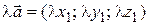 .
.
4°. Длина (модуль) вектора: 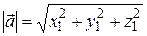 .
.
5°. Условие параллельности векторов: 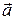 ||
|| 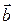 Û
Û 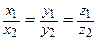 .
.
6°. Чтобы найти координаты вектора надо из координат его конца вычесть координаты начала 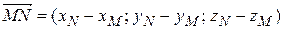 .
.
Пример. Найти длину вектора 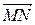 , если
, если 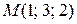 ,
, 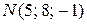 .
.
Решение. По 6°: 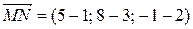 ,
, 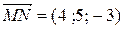 . Его длина (4°):
. Его длина (4°): 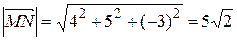 (ед).
(ед).
3. 3. Скалярное произведение векторов есть число, вычисляемое по формуле:
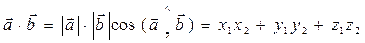 .
.
Угол между векторами:
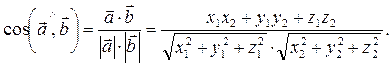
Условие перпендикулярности векторов: 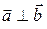 Û
Û 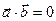 Û
Û 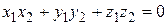 .
.
Проекция вектора 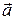 на направление
на направление 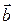 :
: 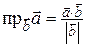 .
.
Пример. Найти угол между векторами 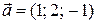 ;
; 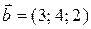 .
.
Решение. Находим 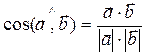 ;
; 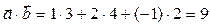 ,
,
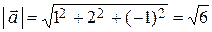 ;
; 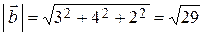 ,
,
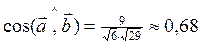 .
.
3. 4. Векторное произведение.
Векторным произведением 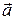 на
на 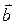 называется вектор
называется вектор 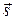 , удовлетворяющим трем условиям
, удовлетворяющим трем условиям
1. 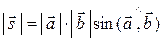 ,
,
2. 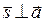 ;
; 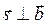 ,
,
3. 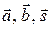 образуют правую тройку, т. е. с конца вектора
образуют правую тройку, т. е. с конца вектора 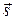 вращение от
вращение от 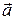 к
к 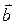 , по наименьшему углу, выглядит против часовой стрелки.
, по наименьшему углу, выглядит против часовой стрелки.
Обозначают 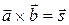 .
.
Обратите внимание, 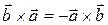 .
.
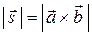 — модуль векторного произведения численно равен площади параллелограмма, построенного на векторах
— модуль векторного произведения численно равен площади параллелограмма, построенного на векторах 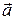 и
и 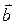 как на сторонах.
как на сторонах.
Если известны координаты сомножителей, то
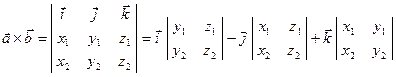 .
.
Пример. Построить векторы 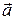 ,
, 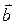 ,
, 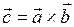 .
.
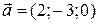 ;
; 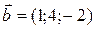 . Найти площадь параллелограмма, построенного на векторах
. Найти площадь параллелограмма, построенного на векторах 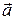 и
и 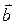 как на сторонах.
как на сторонах.
Решение. Найдем вектор 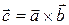 .
.
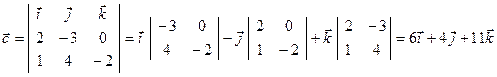 .
.
Сделаем чертеж.
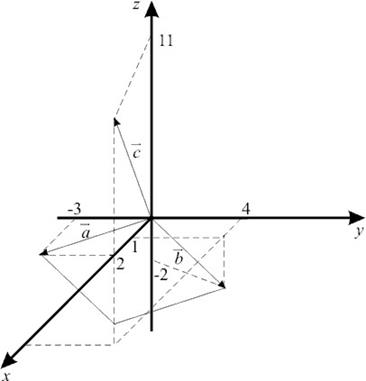
На векторах 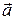 и
и 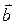 , как на сторонах, строим параллелограмм ОАВD. Его площадь численно равна
, как на сторонах, строим параллелограмм ОАВD. Его площадь численно равна 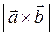 , т. е. длине вектора
, т. е. длине вектора 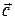 .
.
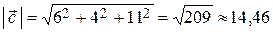
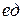 ;
;
Площадь параллелограмма 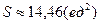 .
.
3. 5. Смешанное произведение трех векторов есть число
.
В координатной форме :
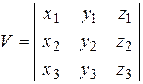 .
.
Модуль смешанного произведения 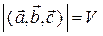 — численно равен объему параллелепипеда, построенного на векторах
— численно равен объему параллелепипеда, построенного на векторах 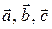 , как на сторонах.
, как на сторонах.
Смешанное произведение имеет знак плюс, если тройка векторов 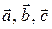 — правая, минус, если тройка левая.
— правая, минус, если тройка левая.
Условие компланарности векторов. Векторы компланарны (лежат в одной плоскости) тогда и только тогда, когда их смешанное произведение равно нулю, т. е.
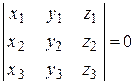 .
.
Дата добавления: 2015-01-29; просмотров: 1414;
