Плоскость и прямая в пространстве
1. Общее уравнение плоскости. Уравнение плоскости есть уравнение первой степени относительно 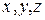 :
:
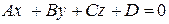 .
.
Вектор 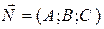 перпендикулярен к плоскости.
перпендикулярен к плоскости.
2. Если плоскость проходит через точку 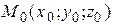 , то ее уравнение
, то ее уравнение
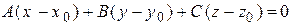 .
.
3. Уравнение плоскости, проходящей через три точки 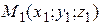 ,
,
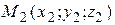 ,
, 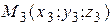 :
:
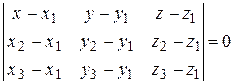
4. Расстояние от точки 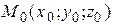 до плоскости
до плоскости 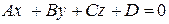 находится по формуле
находится по формуле
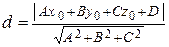
Пример. Найти расстояние до плоскости, проходящей через точки 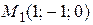 ,
, 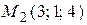 ,
, 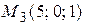 , от начала координат.
, от начала координат.
Решение. Составим уравнение плоскости
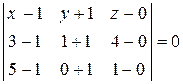 ,
,
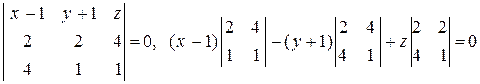
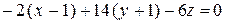 ;
; 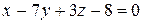 .
.
Расстояние от начала координат 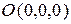 до плоскости
до плоскости
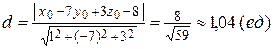 .
.
5. Общие уравнения прямой записываются как линия пересечения двух плоскостей:
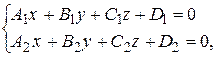
если 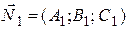 и
и 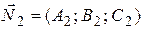 не коллинеарны.
не коллинеарны.
6. Канонические уравнения:
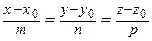
–прямая, проходящая через точку 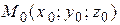 в направлении
в направлении 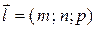 .
.
7. Прямая, проходящая через две данные точки
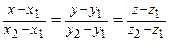
8. Условия параллельности и перпендикулярности плоскостей, прямых, прямой с плоскостью определяются соотношениями направляющих векторов 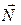 и
и 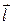 . Например, если плоскости параллельны, то
. Например, если плоскости параллельны, то 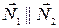 , если прямая параллельна плоскости, то
, если прямая параллельна плоскости, то 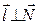 и т. п.
и т. п.
Пример. Через точку 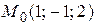 провести прямую, перпендикулярно плоскости
провести прямую, перпендикулярно плоскости 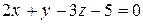 .
.
Решение. Воспользуемся каноническими уравнениями прямой 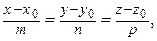
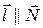 , так как его длина несущественна, можно взять
, так как его длина несущественна, можно взять 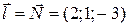 . Имеем
. Имеем 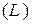 :
: 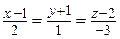 .
.
Пример. Точки 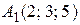 ,
, 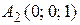 ,
, 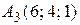 ,
, 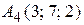 являются вершинами пирамиды. Вычислить 1) длину ребра
являются вершинами пирамиды. Вычислить 1) длину ребра 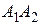 ; 2) угол между ребрами
; 2) угол между ребрами 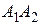 и
и 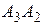 ; 3) площадь грани
; 3) площадь грани 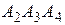 ; 4) Объем пирамиды; 5) уравнения прямой
; 4) Объем пирамиды; 5) уравнения прямой 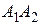 ; 6) уравнение плоскости
; 6) уравнение плоскости  ; 7) уравнение высоты, опущенной из вершины
; 7) уравнение высоты, опущенной из вершины 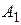 на грань
на грань  ; 8) длину этой высоты.
; 8) длину этой высоты.
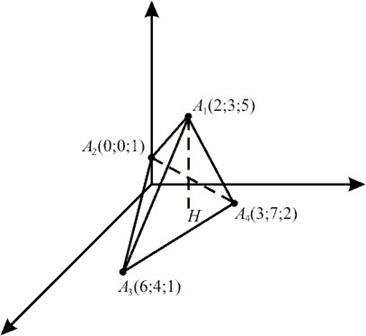
Решение. Найдем координаты векторов — ребер:
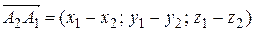 .
.
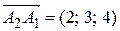 ,
, 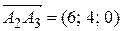 ,
,
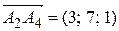 .
.
1) Длина вектора 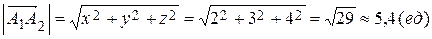 .
.
2) 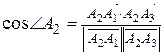 ,
,
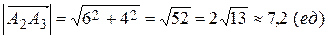 ,
,
Скалярное произведение: 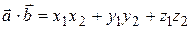 ,
,
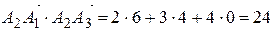 ,
,
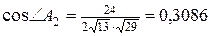 .
.
Из таблиц (или с помощью калькулятора) находим 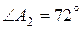 .
.
3) Площадь грани 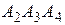 .
.
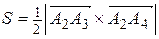
Векторное произведение
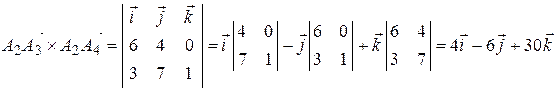 ;
;
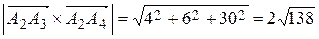 ,
, 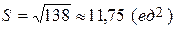
4) Объем пирамиды 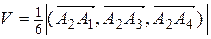 .
.
Смешанное произведение
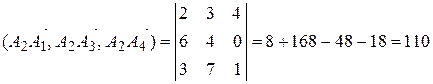 ,
,

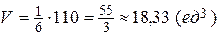 .
.
5) Уравнения прямой 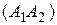 пишем как уравнение прямой, проходящей через две точки:
пишем как уравнение прямой, проходящей через две точки:
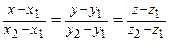 ;
; 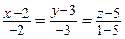 ;
;
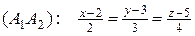 .
.
6) Уравнение плоскости 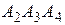 по трем точкам:
по трем точкам:
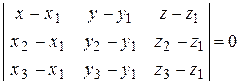 .
.
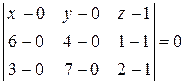 ;
; 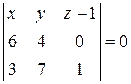 ;
;
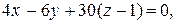
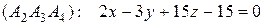 .
. 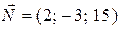
7) Уравнение высоты 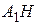 . Канонические уравнения прямой:
. Канонические уравнения прямой:
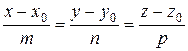 .
.
Прямая проходит через точку 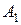 , в качестве направляющего вектора возьмем вектор
, в качестве направляющего вектора возьмем вектор 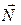 — нормаль к плоскости
— нормаль к плоскости 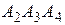 .
.
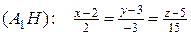
8) Длина высоты может быть найдена как расстояние т. 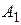 от плоскости
от плоскости 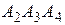
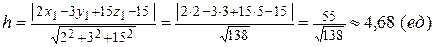
или
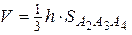 ;
; 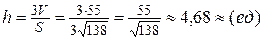 .
.
Дата добавления: 2015-01-29; просмотров: 1096;
