В пространстве

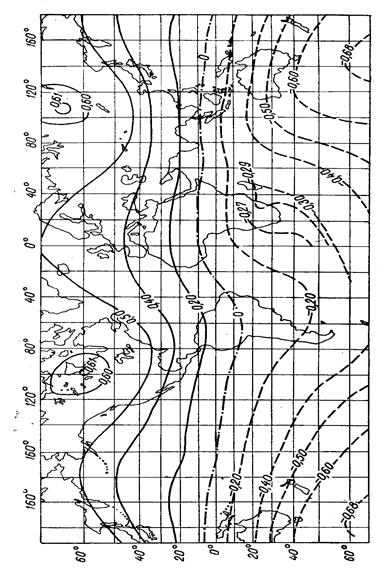
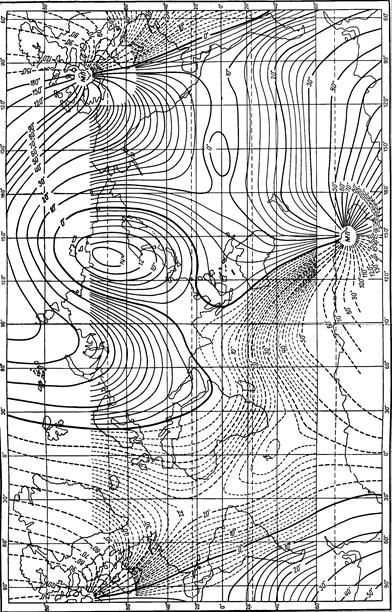
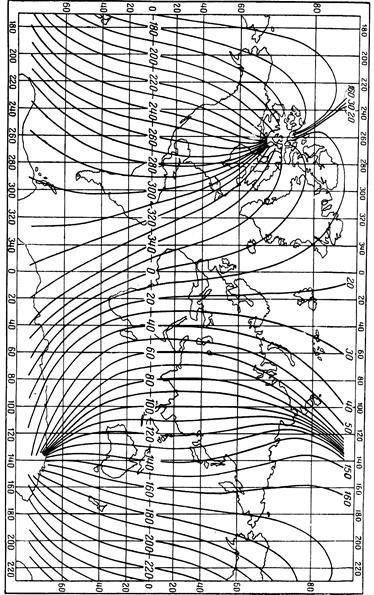
Общее представление о распределении элементов земного магнетизма на поверхности земного шара дают магнитные карты мира (рис. 2.4, 2.5, 2.6, 2.7), опубликованные в открытой зарубежной и отечественной печати для различных эпох. Рассматривая их, можно видеть, что изолинии представляют собой систему кривых, имеющих некоторую закономерность в своем ходе. Так, изогоны, исходя из одной точки земного шара, сходятся в другой, в противоположной. Исключением является область восточной части азиатского материка, где изогоны имеют замкнутый вид. На мировых картах склонения можно выделить линию нулевых значений, называемую огонической. На картах изогон, построенных для районов географических полюсов, можно видеть, что изогоны сходятся не в двух, а в четырех точках, расположенных в северном и южном полушариях. Две из них являются географическими полюсами, а две, находящиеся вблизи географических полюсов, носят название магнитных полюсов.

На магнитных полюсах Н-горизонтальная составляющая равна нулю, а наклонение составляет 90^о. Вследствие этого магнитная стрелка, свободно вращающаяся в горизонтальной плоскости, может устанавливаться в любом направлении, и поэтому использование понятия магнитного меридиана на магнитном полюсе теряет смысл. Склонение на полюсах становится неопределенным и может принимать значения от 0^о до 360^о. Горизонтальная составляющая при переходе от северного магнитного полюса к южному сначала возрастает от нуля (на северном полюсе) до максимальной величины (вблизи экватора), а затем снова убывает от максимума до нуля (на южном полюсе). Максимальная величина на различных меридианах различна. Наибольшая ее величина в области Зондских островов (Н=40 000 нТл).

Наиболее плавный и закономерный ход имеют изоклины, которые представляют собой ряд параллельных кривых, вытянутых в широтном направлении. Нулевая изоклина, называемая магнитным экватором, огибает земной шар и проходит вблизи экватора. По обе стороны от нее наклонение при переходе к магнитным полюсам возрастает от 0 до 90⁰.

Вектор Т на полюсах имеет ориентировку близкую к вертикальной, а на экваторе его направление ориентировано горизонтально. Вектор Т (рис.2.4) в пространстве изменяет свою величину, на экваторе его значение соответствует минимуму – 42 000 нТл, а на полюсе его величина достигает максимума – 70 000 нТл. При изменении широты точки наблюдения происходит изменение величины вектора Т, называемое нормальным градиентом. Составляющие вектора Т тоже могут быть охарактеризованы изменениями в пространстве.

Изолинии вертикальной составляющей имеют ход, аналогичный ходу наклонения. Вблизи магнитных полюсов вертикальная составляющая имеет максимальное значение – около 60 000 нТл, а на магнитном экваторе

величина ее становится равной нулю. По обе стороны от магнитного экватора вертикальная составляющая возрастает по направлению к полюсам, меняя при этом знак: в северном полушарии она положительна, а в южном – отрицательна. В пределах России вертикальная составляющая Z (рис.2.5) изменяется от 40 000 нТл на юге до 60 000 нТл на широте полярного круга. Нормальный градиент Z -составляющей равен около 6 нТл/км. Горизонтальная составляющая Н (рис.2.6) наибольшее значение имеет на юге страны – 28 000 нТл, а к северу уменьшается до 4 000 нТл – в районе полуострова Таймыр.

Положение магнитных полюсов (рис.2.8) точно так же, как и положение изолиний, не является постоянным, а непрерывно меняется.

С удалением от поверхности Земли ее магнитное поле убывает, нормальный вертикальный градиент составляет 20-30 нТл/км. Нормальный градиент Н -составляющей – 4 нТл/км.

За изменением величин элементов земного магнетизма в мировой практике организовано постоянное наблюдение. Измерения ведутся в обсерваториях, в мире их насчитывается более 500. На Урале имеется одна из таких обсерваторий, которая располагается в пос. Арти. Обсерватории оснащены комплектом автоматизированных устройств, которые обеспечивают непрерывное измерение и регистрацию каждого из названных элементов земного магнетизма. Древнейшая из обсерваторий – Лондонская, в ней наблюдения за величиной магнитного склонения ведутся с 1580г.

2.5. Структура магнитного поля Земли

Измеренное магнитное поле на поверхности Земли Т является суммой нескольких полей, имеющих различное происхождение. Связь между ними можно представить формулой

 

Т = Т_о + Т_м + Т_а + Т_в + Т, (2.2)

где Т_о - поле, создаваемое однородной намагниченностью земного шара, оно называется дипольным; Т_м - поле, существование которого вызывается внутренними причинами, связанными с магнитной неоднородностью глубоких слоев земного шара, оно получило название недипольного или материкового, Т_а - поле, формирующееся в условиях обусловленное намагниченности верхних частей земной коры, Т_в - поле, возникающее под влиянием внешних воздействий, и дТ - поле вариаций, связанное с источниками, расположенными вне земного шара.

Сумма дипольного и недипольного полей образует главное магнитное поле Земли, часто его называют нормальным магнитным полем, или государственным нормальным магнитным полем. Поле, обусловленное намагниченностью верхних частей земной коры (Т_а), представляет собой аномальное поле, которое подразделяется на поле регионального характера и поле местного характера, ограниченное по простиранию, т.е. занимает небольшую площадь.

 

 

 

 

 

 

 

 

 

 

 

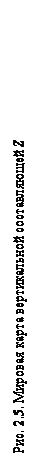
Карты нормального магнитного поля территории России составляются Институтом земного магнетизма, ионосферы и распространения радиоволн РАН (ИЗМИРАН). При построении карт нормального поля применяют метод последовательного сглаживания с осреднением элементов земного магнетизма на определенных площадях. В 1979 г. по данным спутника MAGSAT впервые была построена удачная модель мирового нормального поля. По ее данным уточнены закономерности распространения элементов земного магнетизма на континентальной территории России.

Градиентом нормального поля, или нормальным градиентом, называется изменение нормального поля в заданном направлении. Нормальный градиент элементов Z_а и Н_а в меридиональном направлении составляет 5 нТл на 1 км. Нормальный вертикальный градиент составляет 20-30 нТл/км.

Карты нормального поля используются в магниторазведке в основном для введения поправок в результаты относительных магнитных съемок на больших площадях с целью выявления аномальных значений поля на фоне нормального поля. Для определения значения необходимого элемента нормального геомагнитного поля необходимо снять его значение с изолинии нормального поля, проходящей через данную точку, и ввести поправку за вековой ход. Поправку за вековой ход в данной точке определяют по соответствующей изолинии на карте изопор данного элемента и умножают на разность лет, вычисленную между годом, для которого измерено значение элемента, и эпохой карты нормального поля. Заметим, что вековой ход – это изменение среднегодовых значений какого-либо элемента в течение нескольких лет, отнесенное к единице времени. За единицу времени выбран год.

 

2.6. Аналитическая модель магнитного поля Земли

Магнитные съемки, выполненные в разные годы, необходимо приводить к единой временной эпохе, и кроме того, следует установить единый уровень нормального магнитного поля относительно аномального поля на разобщенных площадях. Для решения задач картографии выбирается представление об аналитической модели главного магнитного поля. Крупным событием в становлении разработки модели магнитного поля Земли стала теория, предложенная К. Гауссом в 1838 г. Данная теория дает возможность представить магнитное поле Земли как функцию координат точки измерения, что позволяет решать ряд задач научного и практического характера. Теория Гаусса в настоящее время снова приобретает актуальное значение в связи с освоением околоземного космического пространства, измерением в нем компонент магнитного поля и привязкой наблюдений к координатам пунктов наблюдений. Аналитическое описание магнитного поля всего земного шара имеет большое научное значение как аппарат для анализа его эволюции и предсказания изменений элементов магнитного поля в будущем.

Чтобы рассмотреть эту теорию, необходимо обратиться к исследованиям, выполненным в 1835 г. русским ученым, профессором Казанского университета И.М.Симоновым. Он сделал предположение, что магнитное поле Земли является полем однородно намагниченного шара, магнитная ось которого проходит через центр земного шара, параллельно линии, соединяющей магнитные полюсы. Решение поставленной задачи заключалось в нахождении поля однородно намагниченного шара как функции координат.

Из теории потенциальных полей /37/ известно, что потенциал однородно намагниченного шара в точке Р выражается формулой

 

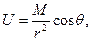(2.3)

где θ – угол между осью магнита ОQ и направлением радиуса-вектора ОР = r (рис.2.9).

 

 

 

Рис.2.9. К выводу потенциала магнитного шара

 

Ось вращения Земли ON составляет с магнитной осью OQ угол 90 – φ₀. Соединяя точки P, Q и N дугами больших кругов, находим из сферического треугольника PQN:

 

 

где φ и λ – широта и долгота точки Р, а φ₀ и λ₀ – широта и долгота точки Q и, следовательно,

 

. (2.4)

 

Представим магнитный момент М как произведение намагниченности J и объема шара:

 

 

где R – радиус шара.

 

Если введем следующие обозначения:

 

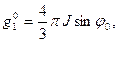
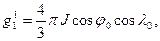( 2.5)

 

то получим

 

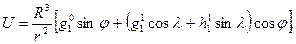. (2.6)

 

Так как дуга большого круга NP является меридианом точки P, то составляющая в направлении NP будет не чем иным, как северной составляющей X, а составляющая в направлении дуги малого круга PS, являющаяся параллелью, будет восточной составляющей Y, а составляющая в направлении радиуса вектора r будет вертикальной составляющей Z. Поэтому получим следующие закономерности:

 

(2.7)

 

К.Ф.Гаусс в 1938 г. сделал предположение, что магнитное поле Земли вызывается источниками, находящимися внутри земного шара, имеющими потенциальный характер. В этом случае магнитный потенциал шара можно записать в следующем виде:

 

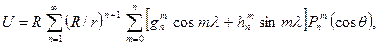(2.8)

 

где R – радиус Земли, r, θ и λ - сферические координаты точки (начало координат в центре Земли, r – расстояние от центра Зем

ли, θ – дополнение широты до 90⁰, λ - восточная долгота), g_n^m и h_n^m - постоянные коэффициенты Гаусса; P_n^m(cosθ) – присоединенный полином Лежандра степени n и порядка m. Для точек, находящихся на поверхности земного шара (r=R), магнитный потенциал можно переписать в виде

 

. (2.9)

 

Теория Гаусса лежит в основе сферического гармонического анализа магнитного поля Земли. Модель поля фиксированной эпохи конструируется путем усечения рядов формулы (2.9) по n, а их параметры определяются по измеренным значениям элементов земного магнетизма X, Y и Z на поверхности Земли. Задача сводится к решению системы линейных уравнений относительно коэффициентов Гаусса, которые определяются либо методом наименьших квадратов, либо интегральными методами, основанными на свойстве ортогональности сферических функций.

Формула Гаусса (2.9) дает возможность при известных коэффициентах g_n^m и h_n^m определить величину магнитного момента земного шара, его направление и градиенты элементов земного магнетизма в любой точке пространства. Магнитный момент земного шара по этим коэффициентам можно определить так:

 

.

 

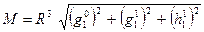Измерения, проводимые на земной поверхности и в космосе, позволяют определять коэффициенты гауссового ряда. С учетом изменения их величин во времени Международная ассоциация по геомагнетизму и аэрономии каждые пять лет утверждает модель, именуемую Международным аналитическим эталонным полем.

 

Магнитное поле планет солнечной системы

Магнетизм планет земной группы резко отличен от земного. У Венеры напряженность магнитного поля на экваторе составляет 3 нТл, у Марса – 40-60 нТл, у Меркурия она достигает 170 – 330 нТл. Магнитные моменты у этих планет не превышают тысячных долей магнитного момента Земли, поэтому исследователями сделано предположение, что магнитные поля планет создаются остаточной намагниченностью их литосфер, приобретенной в полях молодой солнечной системы или в полях ранее действовавших динамо-процессов в ядрах этих планет. Измерения на межпланетных космических аппаратах дают право предположить, что механизмы динамо-генерации магнитных полей планет–гигантов Юпитера и Сатурна аналогичны механизмам возникновения магнитного поля Земли.