ГЛАВА 2
Электропроводность (способность проводить ток под действием постоянного электрического поля) растворов электролитов обусловлена переносом вещества (направленным движением ионов) и его химическими превращениями. В этом случае раствор называется проводником второго рода. Электропроводность такого раствора зависит, прежде всего, от природы электролита (от подвижности ионов), его концентрации в растворе, вязкости и температуры самого раствора и др. В проводниках первого рода (к ним относятся преимущественно металлы) переноса вещества не происходит.
Согласно теории Аррениуса, электролиты в водном растворе диссоциируют на заряженные частицы – ионы, которые и являются переносчиками электричества. Не все электролиты диссоциируют в одинаковой степени: одни – сильные электролиты, диссоциируют в растворе полностью; другие – слабые электролиты – лишь частично. В последнем случае доля распавшихся молекул, называемая степенью диссоциации (a), зависит от концентрации электролита и температуры.
В растворе слабого электролита между недиссоциированными молекулами и ионами устанавливается равновесие:
KnAm « nKm+ + mAn-
Для бинарного электролита: КА « К+ + А-
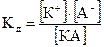
Константа равновесия процесса электролитической диссоциации называется константой диссоциации (Кд).
Положим, что степень диссоциации равна a. Если концентрация кислоты в растворе равна С (моль/л), то концентрации катиона и аниона равны aС, а концентрация недиссоциированной части (1-a)С. Поэтому
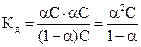, (6.1)
Вычисленная практическая константа Кд зависит от концентрации. Независимой от концентрации является термодинамическая константа диссоциации, выраженная через активность ионов и молекул:
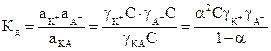, (6.1/)
где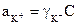 
- активность ионов К+, 
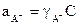- активность ионов А-, 
, 
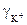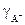- коэффициенты активности соответствующих ионов, с – концентрация электролита.
Ионы в растворе электролита находятся в непрерывном беспорядочном движении. При наложении внешнего электрического поля на хаотичное движение ионов накладывается ориентированное поступательное движение к поверхности электродов: катионов – к отрицательному, а анионов – к положительному электроду. В результате возникает электрический ток.
Величина, характеризующая способность веществ проводить электрический ток под действием внешнего электрического поля, называется электрической проводимостью.
Электрическая проводимость (L) – величина, обратная электрическому сопротивлению проводника (R). Измеряется в сименсах (См): См=Ом-1.
Так как
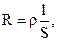
то
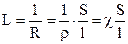, (6.2)
где r - удельное сопротивление; c - удельная электрическая проводимость; S – площадь сечения проводника; l – длина проводника.
Электрическая проводимость в растворах электролита зависит от числа ионов в объеме раствора между электродами и скорости их движения.
Для оценки проводимости растворов и влияния на нее различных факторов применяют две величины: удельную (c) и молярную (l) электрическую проводимость.
Удельной электрической проводимостью (c) называют электропроводность раствора, находящегося между параллельными электродами площадью 1 см2, расположенными на расстоянии 1 см.
Удельная электрическая проводимость измеряется в См×см-1 или См×м-1.
Молярная электрическая проводимость – мера электрической проводимости всех ионов, образующихся при диссоциации 1 моля электролита при данной концентрации.
Молярная электрическая проводимость равна электрической проводимости такого объема (V, см3) раствора, в котором содержится 1 моль растворенного вещества, причем электроды находятся на расстоянии 1 см друг от друга.
Удельная и молярная электрические проводимости связаны соотношением:
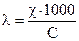, (6.3)
где С – концентрация, моль×дм-3; l- молярная электрическая проводимость, См×см2×моль-1; c - удельная электрическая проводимость, См×см-1.
Поскольку электрическая проводимость объема раствора электролита определяется количеством в этом объеме ионов, переносящих электричество, и скоростью их миграции, для молярной проводимости справедливо соотношение:
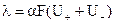, (6.4)
где U+, U- - абсолютные скорости движения ионов (т.е. скорости их передвижения в поле с напряженностью 1 В·см-1); a - степень диссоциации электролита; F – число Фарадея, т.е. количество электричества, которое несет 1 моль однозарядных катионов или анионов.
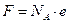
где NA = 6×1023 – число Авогадро, е – 1,6×10-19 Кл – заряд электрона.
При разбавлении раствора молярная электрическая проводимость как сильных, так и слабых электролитов возрастает: для слабых электролитов – вследствие увеличения степени диссоциации (a), для сильных – в результате повышения абсолютной скорости движения ионов (U+, U-).
Предельное значение l0, отвечающее молярной электрической проводимости гипотетического бесконечно разбавленного раствора, характеризующегося полной диссоциацией электролита и отсутствием сил электростатического взаимодействия между ионами, в соответствии с (6.4) может быть выражено соотношением:
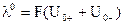(6.5)
Произведения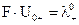 
и 
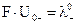называются предельными молярными проводимостями, или предельными подвижностями катионов и анионов. Уравнение (6.5) можно записать в виде:
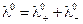. (6.6)
Молярная электрическая проводимость электролита при бесконечном разбавлении (l0) равна сумме предельных подвижностей анионов и катионов.
Соотношение (6) установлено Кольраушем и называется законом независимого движения ионов.
Предельная подвижность ионов зависит только от природы растворителя и температуры; для многих ионов эта величина экспериментально определена и приведена в справочниках.
Молярная электрическая проводимость растворов слабых электролитов меньше, чем сильных. Это связано с тем, что даже при низких концентрациях степень диссоциации слабых электролитов мала (a<1), следовательно, несмотря на то, что в объеме раствора, заключенного между электродами, содержится 1 моль электролита, ионов-переносчиков электрического тока в этом объеме меньше, чем в растворе сильного электролита. Повышение молярной электрической проводимости слабых электролитов при разбавлении растворов связано именно с увеличением степени диссоциации.
Из уравнений (6.4) и (6.5) следует:
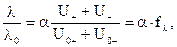(6.7)
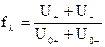- коэффициент электрической проводимости, характеризующийся степенью торможения ионов.
Абсолютные скорости движения ионов в разбавленных растворах электролитов (U+, U-) и в бесконечно разбавленных (U0+, U0-) близки между собой (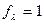 
), поэтому
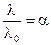(6.8)
Таким образом, степень диссоциации электролита в растворе заданной концентрации можно рассчитать, если измерить молярную электрическую проводимость этого раствора и знать l0, которую можно рассчитать по формуле (6.5).
Электродными процессами называют химические превращения, происходящие в растворе на электродах из проводников первого рода.
Гальванический элемент – прибор, преобразующий энергию химической реакции в электрическую. Он состоит из двух электродов, погруженных в растворы своих солей. Между каждым электродом и раствором возникает разность потенциалов. Если растворы соединить мостиковым контактом через насыщенный раствор, например, хлористого калия, то это обеспечит возможность электрической проводимости между ними при отсутствии их взаимодиффузии. Если эти электроды соединить, например, медной проволокой, то на одном из электродов пойдет реакция окисления, а на другом – реакция восстановления. Возникающая при этом разность потенциалов между электродами называется электродвижущей силой (ЭДС) элемента. ЭДС гальванического элемента равна разности электродных потенциалов:
ε = E1 – E2. (6.9)
где ε – электродвижущая сила гальванического элемента, В;
E – электродный потенциал, В.
Величина электродного потенциала зависит от природы электролита, концентрации раствора и температуры (формула Нернста):
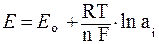,(6.10)
где Ео – стандартный электродный потенциал, т.е. потенциал при активности (а) образующих потенциал ионов, равной единице, В;
n – заряд иона или число электронов;
F – число Фарадея, Кл · моль–1;
nF – перенесенное количество электричества;
a i – активность иона, которая для сильноразбавленных растворов может быть заменена его концентрацией.
Для расчета величины ЭДС используется уравнение Нернста, которое для гальванического элемента, где протекает окислительно-восстановительная реакция, записанная в общем виде:
a A + b B = c C + d D,
в условиях равновесия будет выглядеть так:
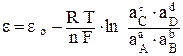,(6.11)
где εо – стандартное значение ЭДС, В;
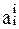– активности веществ, участвующих в участников реакции.
ГЛАВА 2
Дата добавления: 2015-02-16; просмотров: 551;