Графоаналитическое разложение кривых в ряд Фурье

Когда несинусоидальная кривая задана графиком или таблицей и не имеет аналитического выражения, для определения её гармоник прибегают к графоаналитическому разложению. Оно основано на замене определенного интеграла суммой конечного числа слагаемых. С этой целью период функции f(ωt) разбивают на n равных частей Δωt=2π/n (рис.6.6).

Тогда для нулевой гармоники

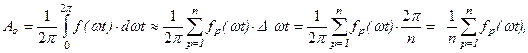
где: р – текущий индекс (номер участка), принимающий значения от 1 до n;

f_р(ωt) – значение функции f(ωt) при ωt=р·Δωt (см. рис.6.6).

Для амплитуды синусной составляющей k–ой гармоники

.

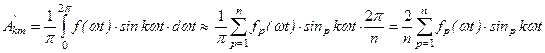Для амплитуды косинусной составляющей k–ой гармоники

.

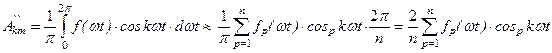Здесь sin_pkωt и cos_pkωt - значения sinkωt и coskωt при ωt=р·.

В практических расчетах обычно принимают n=18 (Δωt=20˚) или n=24 (Δωt=15˚).

При графоаналитическом разложении кривых в ряд Фурье еще важнее чем при аналитическом выяснить, не обладает ли она каким-либо видом симметрии, наличие которых существенно уменьшает объем вычислительной работы. Так, формулы для 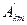и при наличии симметрии принимают вид

.

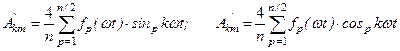При построении гармоник на общем графике необходимо учитывать, что масштаб по оси абсцисс для k–ой гармоники в k раз больше, чем для первой.

Лекция №29. Максимальное, среднее и действующее значения несинусоидальных величин

Цель: выдать более глубокие знания по цепям переменного тока.

Задача: научить определять параметры цепей периодичного несинусоидального тока.

Периодические несинусоидальные величины, помимо своих гармонических составляющих, характеризуются максимальным, средним и действующим значениями. Максимальное значение А_m– это наибольшее в течение периода значение модуля функции (рис.6.7).

Среднее по модулю значение определяется так

.

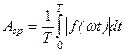Если кривая симметрична относительно оси абсцисс и в течение полупериода ни разу не изменяет знак, то среднее по модулю значение равно среднему значению за полпериода

,

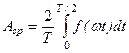причем в этом случае начало отсчета времени должно быть выбрано так, чтобы f(0)=0.

Если функция за весь период ни разу не изменяет знак, то её среднее по модулю значение равно постоянной составляющей.

В цепях несинусоидального тока под величинами ЭДС, напряжений или токов понимают их действующие значения, определяемые по формуле

.

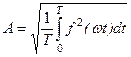Если кривая разложена в ряд Фурье, то её действующее значение может быть определено следующим образом

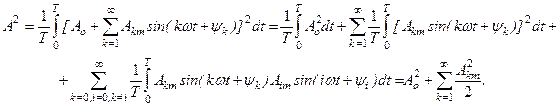
Поясним получение результата. Произведение синусоид разной частоты (kω и iω) представляет собой гармоническую функцию, а интеграл за период от любой гармонической функции равен нулю. Интеграл, находящийся под знаком первой суммы, определялся в цепях синусоидального тока и там было показано его значение. Следовательно,

.

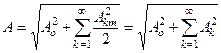Из этого выражения вытекает, что действующее значение периодических несинусоидальных величин зависит только от действующих значений её гармоник и не зависит от их начальных фаз ψ_k.

Приведем пример. Пусть u=120 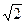sin(314t+45˚)-50 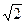sin(3·314t-75˚) B. Его действующее значение

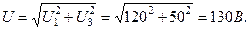
Бывают случаи, когда среднее по модулю и действующее значения несинусоидальных величин могут быть рассчитаны на основании интегрирования аналитического выражения функции и тогда нет необходимости раскладывать кривую в ряд Фурье.

В электроэнергетике, где кривые преимущественно симметричны относительно оси абсцисс, для характеристики их формы используется ряд коэффициентов. Наибольшее применение получили три из них: коэффициент амплитуды k_а, коэффициент формы k_ф и коэффициент искажения k_и. Они определяются так: k_а=A_m/A; /A_ср; k_и=A₁/A.

Для синусоиды они имеют следующие значения: k_а= 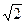; k_ф=πA_m/2 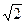A_m≈1.11; 1.

Для кривой прямоугольной формы (рис.6.8,а) коэффициенты таковы: k_а=1; k_ф=1; k_и=1.26/ .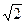

Для кривой заостренной (пикообразной) формы (рис.6.8,б) значения коэффициентов следующие: k_а> 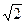и тем выше, чем более пикообразной является её форма; k_ф>1.11 и тем выше, чем заостреннее кривая; k_и<1 и чем более заостренная кривая, тем меньше.

Как видим рассмотренные коэффициенты в определенной степени характеризуют форму кривой.

Укажем одно из практических применений коэффициента искажения. Кривые напряжения промышленных сетей обычно отличаются от идеальной синусоиды. В электроэнергетике вводится понятие практически синусоидальной кривой. По ГОСТ напряжение промышленных сетей считается практически синусоидальным, если наибольшее отличие соответствующих ординат истинной кривой и её первоё гармоники не превышает 5% от амплитуды основной гармоники (рис.6.9).

Измерение несинусоидальных величин приборами различных систем дает неодинаковые результаты. Амплитудные электронные вольтметры измеряют максимальные значения. Магнитоэлектрические приборы реагируют только на постоянную составляющую измеряемых величин. Магнитоэлектрические приборы с выпрямителем измеряют среднее по модулю значение. Приборы всех остальных систем измеряют действующие значения.