Дискретное преобразование Фурье
Резервы для уменьшения цифрового потока без ущерба качеству воспроизво-димого изображения заключены в специфике ТВ сигнала, обладающего значительной информационной избыточностью, которую условно делят на пространственную (статистическую, внутрикадровую), психофизическую (физиологическую) и временную (межкадровую) [5,8,10]. Следует также отметить, что резких границ здесь нет. Психофизическая избыточность связана и с временной и пространственной избыточностями.
Примером сокращения психофизической избыточности может служить способ передачи градаций яркости от крупных и мелких деталей (внутрикадровая избыточность) и особенности восприятия движущихся объектов (межкадровая избыточность).
Пространственная (статистическая) избыточность обусловлена наличием в изображении тесных связей (однотонных одинаково окрашенных участков).Отсчеты видеосигнала в соседних точках (элементах) на таких участках практически одинаковы или слабо изменяются в плоскости изображения, что позволяет заметно сократить число битов, необходимое для отображения кадра изображения.
Временная избыточность изображения проявляется в относительно малом отличии двух последовательных кадров ТВ изображения. Здесь передаваемый массив информации можно сократить, если содержание одного кадра (поля), называемого опорным, передавать целиком, а вместо следующего кадра передавать только информацию о переместившихся объектах в их новых положениях.
Физиологическая избыточность ТВ сигнала обусловлена ограниченностью возможностей зрительного аппарата. Использовать физиологическую избыточность - значит не передавать в сигнале ту информацию, которая не будет воспринята нашим зрением. Например, наш глаз мелкие детали в цвете не видит, а различает их только по яркостным оттенкам. Поэтому цветоразностные сигналы передаются в более узкой полосе частот, чем яркостный сигнал.
В большинстве случаев видеопоследовательности (ТВ изображение) содержат статистическую избыточность в двух направлениях – временном и пространственном. Главное статистическое свойство, на котором основана аппаратура сжатия - межэлементная корреляция, включающая предположение о коррелированности последовательных кадров видеоданных. Таким образом, значения отдельных элементов изображения могут быть предсказаны либо по значениям ближайших элементов внутри одного кадра (внутрикадровое кодирование), либо по значениям элементов, расположенных в ближайших кадрах (межкадровое кодирование и компенсация перемещения).
В некоторых случаях, например, при смене сюжета, временная корреляция между ближайшими кадрами очень низка. В таких случаях решающую роль играет внутрикадровая корреляция, то есть пространственная корреляция элементов изображения. Однако, если корреляция между последовательными кадрами видеоданных высока, желательно устранить межкадровую избыточность. При этом применяемые методы преобразования изображения основаны на том, что его цифровой эквивалент (сигнал ИКМ) приводится к виду, удобному для сокращения избыточной информации. Наиболее эффективным методом является преобразование видеоинформации из временной области в спектральную. Результат преобразования представляет собой совокупность спектральных коэффициентов, которые характеризуют амплитуды пространственных частот изображения.
Из различных ортогональных преобразований стандартом MPEG рекомендовано использовать дискретно-косинусное преобразование (ДКП), являющееся частным случаем двумерного преобразования Фурье.
Преобразование Фурье - это метод обработки, который анализирует изменение сигнала во времени, выражает их в виде частотного спектра. Любой сигнал можно разложить на частотные гармонические составляющие и затем по известным значениям амплитуды и фазы этих составляющих линейным суммированием их восстановить исходный сигнал.
Эту операцию называют обратным преобразованием Фурье. В цифровых системах сигнал выражается последовательностью во времени дискретных отсчетов (рис. 5.37,а). При использовании преобразования Фурье для фрагмента цифрового сигнала из некоторого числа отсчетов (рис. 5.37,а), последний можно разложить на такое же число дискретных частот (рис. 5.37,б). Это преобразование называют дискретным преобразованием Фурье.
Поскольку любое изображение или его фрагмент в телевидение можно рассматривать как функцию изменения яркости (или цветности ) как по оси Х, так и по оси У, то дискретное ортогональное преобразование Фурье заменяет массив этих отсчетов изображения (рис. 5.37,а) соответствующего фрагмента на массив коэффициентов (рис. 5.37,б), соответствующих амплитудам частотных составляющих Фурье. ДКП осуществляет перевод отдельных блоков изображения из пространственной области значений сигнала в область пространственных частот спектральной плоскости (рис. 5.37,б). В результате массиву исходных значений сигнала (рис. 5.37,а) соответствует массив из такого же числа коэффициентов, представляющих собой амплитуды этих косинусных составляющих (рис. 5.37,б).
Так как объем машинных расчетов для нахождения этих коэффициентов весьма значителен, то ДКП Фурье осуществляется над небольшими по размеру фрагментами изображения - 8 х 8 элементов. Для минимизации вычислений ДКП использует в качестве набора преобразующих функций (базисных) только косинусные составляющие. В результате массиву исходных значений сигнала (рис. 5.37,а) соответствует массив из такого же числа коэффициентов, представляющих собой амплитуды этих косинусных составляющих (рис. 5,37,б) [18,5].
Двумерное ДКП ведется по формуле [5]:
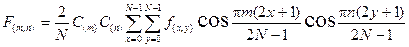 , (5.6)
, (5.6)
где 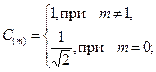
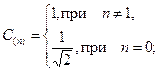
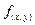 - отсчеты изображения с пространственными координатами x,y (от 0 до N-1); N- размер блока изображения (N xN элементов);
- отсчеты изображения с пространственными координатами x,y (от 0 до N-1); N- размер блока изображения (N xN элементов); 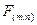 - коэффициенты, характеризующие изображения в спектральной плоскости m,n (от 0 до N-1).
- коэффициенты, характеризующие изображения в спектральной плоскости m,n (от 0 до N-1).

Рис. 5.37. Преобразование блока изображения 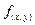 в блок коэффициентов
в блок коэффициентов 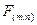 :
:
а) – блок изображения, б) – блок коэффициентов ДКП
ДКП является обратимым: по распределению 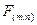 обратным преобразованием однозначно восстанавливается в декодирующем устройстве
обратным преобразованием однозначно восстанавливается в декодирующем устройстве 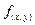 из имеющихся трансформант:
из имеющихся трансформант:
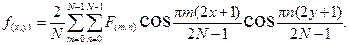 (5.7)
(5.7)
Квантование является важным звеном обработки сигнала, на котором происходят потери. Оно определяет точность хранения результатов ДКП и коэффициент сжатия. При квантовании каждое из значений ДКП делится на коэффициент квантования 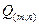 , индивидуальный для каждой пространственной частоты, который берется из заранее определенной таблицы коэффициентов квантования размером 8х8 (естественно, она должна быть одинаковой для кодера и декодера). Эта таблица может быть взята по умолчанию или формируется кодером для конкретных изображений и передается декодеру вместе со сжатыми данными. Для сигнала цветного изображения таблицы могут различаться для разных компонент (
, индивидуальный для каждой пространственной частоты, который берется из заранее определенной таблицы коэффициентов квантования размером 8х8 (естественно, она должна быть одинаковой для кодера и декодера). Эта таблица может быть взята по умолчанию или формируется кодером для конкретных изображений и передается декодеру вместе со сжатыми данными. Для сигнала цветного изображения таблицы могут различаться для разных компонент ( 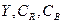 ). При декодировании исходные величины приближенно восстанавливаются путем умножения на фактор квантования. Сказанное поясняется табл. 5.3 [13].
). При декодировании исходные величины приближенно восстанавливаются путем умножения на фактор квантования. Сказанное поясняется табл. 5.3 [13].
Из таблицы видно, что восстановленное изображение отличается от оригинала незначительно.
Рассмотренные виды избыточности ТВ сигнала и способы их устранения использованы в стандартах описания цифрового потока в канале связи JPEG, MPEG, и других стандартах.
Таблица 5.3 Фазы преобразования сигналов блока изображения (8*8) при ДКП и их восстановление в декодере
| 139 144 149 153 155 155 155 155 144 151 153 156 159 156 156 156 150 155 160 163 158 156 156 156 159 161 165 160 160 159 159 159 159 160 161 162 162 155 155 155 161 161 161 161 160 157 157 157 162 162 161 163 162 157 157 157 162 162 161 161 163 158 158 158 | 1260 -1 -12 -6 2 -2 -2 2 -22 -17 -6 -3 -3 0 1 -1 -11 -10 -1 2 1 -1 -1 -1 -7 -2 0 2 1 0 0 0 0 -1 1 1 -1 -1 1 2 2 0 1 -1 -1 2 2 0 -1 -1 0 -1 0 2 1 -1 -3 1 -3 -1 2 1 -1 -1 |
| Выборки оригинала | Коэффициенты ДКП(округлены) 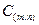
|
| 8 11 10 16 24 40 51 61 12 12 14 19 26 58 60 55 14 13 16 24 40 57 69 56 14 17 22 29 51 87 80 62 18 22 37 56 68 109 103 77 24 35 55 64 81 104 113 92 49 64 78 87 103 121 120 101 72 92 95 98 112 100 103 99 | 158 0 -1 0 0 0 0 0 -2 -1 0 0 0 0 0 0 -1 -1 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
Таблица квантования 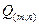
| Коэффициент после квантования 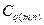
|
| 1264 0 -10 0 0 0 0 0 -24 -12 0 0 0 0 0 0 -14 -13 0 0 0 0 0 0 -14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 142 144 147 150 152 153 154 154 149 150 153 155 156 157 156 156 157 158 159 161 161 160 159 158 162 162 163 163 162 160 158 157 162 162 162 162 161 158 156 155 160 161 161 161 160 158 156 154 160 160 161 162 161 160 158 157 160 161 163 164 164 163 161 160 |
Коэффициенты после обратного квантования 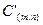
| Восстановленные величины отсчетов |
| -2 | -3 | -3 | -2 | -1 | -1 | ||||
| -1 | -1 | -3 | |||||||
| -1 | -2 | ||||||||
| -2 | -1 | -2 | |||||||
| -1 | |||||||||
| -1 | -1 | -3 | |||||||
| -2 | -2 | -1 | -1 | ||||||
| -2 | -1 | ||||||||
| Погрешности восстановления отсчетов |
Дата добавления: 2015-03-20; просмотров: 1738;
