ДЕТАЛЬНАЯ РАЗБИВКА КРУГОВЫХ КРИВЫХ
Детальная разбивка кривой предусматривает не только закреп-ление на местности начала НК, конца КК и середины СК кривой, но и обозначение всей кривой, например, колышками через определен-ный интервал. Существует ряд способов разбивки круговых кривых: способ прямоугольных координат, способ углов, способ продолжен-ных хорд.
Способ прямоугольных координат (ординат от тангенса).
| Пусть необходимо обозначить на мест-ности точки 1, 2, 3 и т.д. через определен-ный интервал, равный длине дуги К.
Если принять ус-ловную систему коор-динат Х-НК-У, то по-ложение каждой точ-ки определится пря-моугольными коор-динатами:
| |
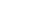


точка 1 : Х1 = R sin j1 , Y1 = R – R cos j1 = 2R sin2 j1/2 ,
точка 2 : Х2 = R sin2j1 , Y2 = R – R cos2j1 = 2R sin2 2j1/2 ,
точка 3 : Х3 = R sin3j1 , Y3 = R – R cos3j1 = 2R sin2 3j1/2 ,
…………………………………………………………….
точка n : Хn = R sinnj1 , Yn = R – R cosnj1= 2R sin2 nj1/2 .
В эти формулы подставляют значение угла j1, зависящее от величины интервала К, которое можно найти из выражения:
j1= 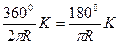 .
.
На местности откладывают от начала кривой НК по направ-лению на вершину угла поворота ВУ (по направлению тангенса) абсциссы Хi , а по перпендикулярному направлению ординаты Уi и закрепляют точки 1, 2, 3 и т.д. Так производят разбивку до середины кривой. Другую половину кривой разбивают с ее конца. Для определения координат Х и У существуют специальные таблицы.
Этот способ применяется на ровной площадке и является наиболее точным, так как точки 1, 2, 3 и т.д. выносят независимо друг от друга, поэтому ошибка положения одной точки не окажет влияния на положение других точек, чего нельзя сказать о рассмат-риваемых далее способах углов и продолженных хорд .
Способ углов (полярный способ).
| Теодолит устанавливают в точке НК и приводят его в рабочее положение. Зритель-ную трубу ориентируют по направлению на ВУ так, чтобы отсчет на лимбе был равен 0°00’ и лимб закрепляют.
Откладывают на лимбе угол j1/2 и закрепляют на рас-стоянии S точку 1 так, чтобы она попала в перекрестие сет-ки нитей. Далее откладывают угол 2j1/2 и на расстоянии S от точки 1 закрепляют точку 2 и т.д.
| |
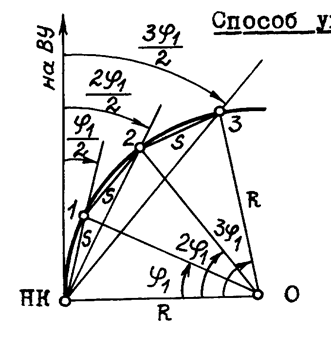
Этот способ удобно применять в стесненных условиях, когда есть видимость между НК и точками 1, 2, 3,... (например, на высокой насыпи, где способ прямоугольных координат неприемлем).
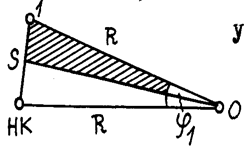
Угол j1 может быть найден по формуле 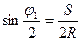 (из решения заштрихованного треугольника), причем в этом способе S явля-ется хордой определенной длины. (из решения заштрихованного треугольника), причем в этом способе S явля-ется хордой определенной длины.
| |

Способ продолженных хорд
| перемещение b и закрепля-ют точку 2 также на рас-стоянии S от точки 1.
Далее в створе 1-2 на расстоянии S отмечают точку 3' и отрезками b и S засекают точку 3 и т.д. Ве-личина b = S2/R, что выте-кает из подобия треуголь-ников 1-2-О и 1-2-2’ .
Часто для вынесения точки 1 принимают Х1 » S ,
а У1 » b/2.
| |
Вначале по координатам Х1 и У1 выносят точку 1. Затем в створе НК-1 на расстоянии S от точки 1 отмечают вспомогательную точку 2’, от которой откладывают так называемое промежуточное




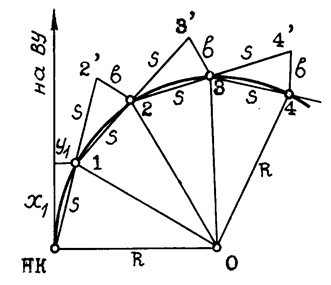
Этим способом одну половину кривой разбивают с HK, а дру-гую половину - с конца кривой КК. Способ применим в любыхстес-ненных условиях, в том числе и в выемке, где первые два способа неприемлемы.
Недостатком способов углов и продолженных хорд является снижение точности разбивки кривой по мере возрастания ее длины, так как положение каждой последующей точки определяется относительно предыдущей.
Дата добавления: 2015-02-28; просмотров: 8174;



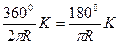 .
.

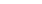







 (из решения заштрихованного треугольника), причем в этом способе S явля-ется хордой определенной длины.
(из решения заштрихованного треугольника), причем в этом способе S явля-ется хордой определенной длины.