Дифференциальные уравнения переноса субстанции в движущейся жидкости (Навье-Стока, Фурье-Кирхгофа и Фика).

Запишем уравнение переноса импульса для несжимаемой вязкой (идеальной) жидкости объемом 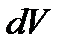для оси z (уравнение Навье-Стока для нестационарного потока):

где 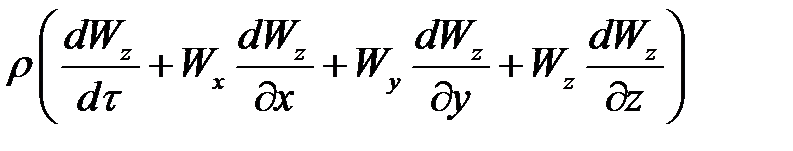- сила инерции;

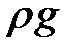- сила тяжести;

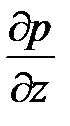- сила давления;

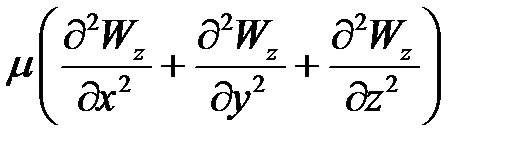- сила внутреннего трения;

W_x, W_y, W_z - проекции скорости на оси координат.

С одной стороны, уравнение можно трактовать как баланс сил, действующих на элементарный движущийся объем жидкости, с другой стороны, уравнение – это ОБС.

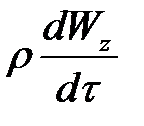- локальное накопление (в данной точке) импульса во времени;

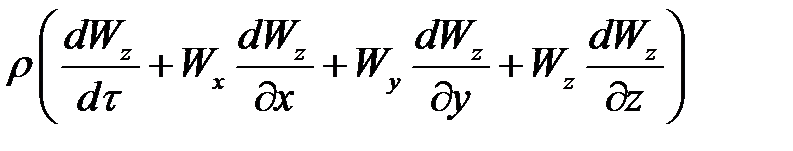- накопление импульса за счет конвекции, т.е. при перемещении объема dV;

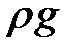- источник (или сток) импульса в контуре за счет силы гравитации;

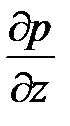- накопление импульса за счет силы давления;

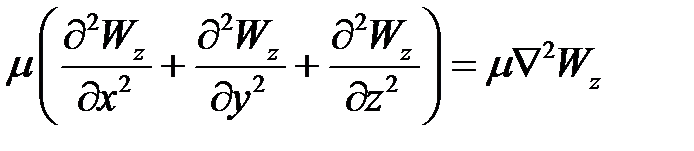- накопление импульса за счет силы внутреннего трения;

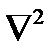- оператор Лапласа (лапласиан), т.е. сумма вторых производных по координатным осям.

Запишем уравнение переноса теплоты в движущейся жидкости( 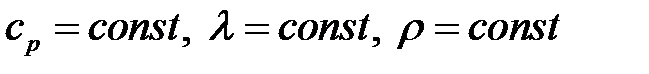, среда – однофазная, неразрывная, изотропная) (уравнение Фурье-Кирхгофа для нестационарного потока):

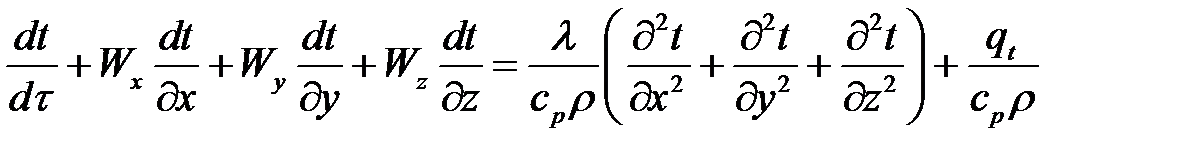
соответствует локальному накоплению теплоты во времени средой объемом dV за счет изменения температуры в данной точке;

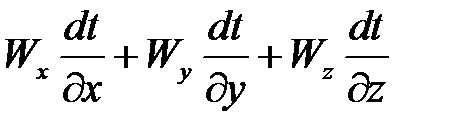отвечает накоплению теплоты за счет конвекции;

выражает перенос теплоты кондукцией (теплопроводностью).

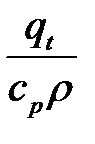характеризует теплопоглощение (тепловыделение) внутри контура dV;

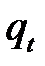- источник (или сток) теплоты в единице объема и в единицу времени [Дж/м³·с].

Запишем уравнение переноса вещества (массы) в движущейся жидкости(D = const, среда однофазная, изотропная, неразрывная) (уравнение Фика для нестационарного потока):

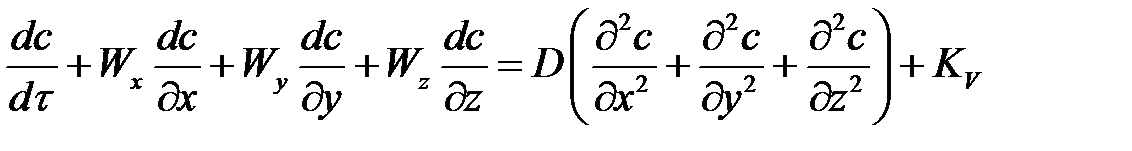
с – концентрация вещества [с] = [кмоль/м³];

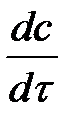соответствует локальному накоплению вещества во времени за счет изменения его концентрации в данной точке;

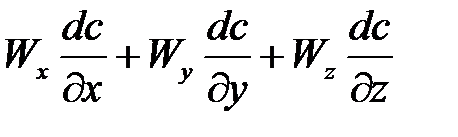отвечает накоплению вещества за счет конвекции;

характеризует молекулярный перенос компонента;

K_V выражает возникновение (исчезновение) вещества в объеме dV в результате химического превращения.