Преобразование исходной матрицы решений
Целый ряд критериев требует преобразования исходной матрицы, ее дополнения вероятностным описанием компонентов. Преобразуем матрицу решений с учетом вероятности появления условия х.
Сгенерируем закон распределения, близкий к ожидаемому ps, скорректируем ps1, пронормируем p:
В качестве ожидаемого распределения вероятности проявления условия осуществления решения принято ХИ-квадрат распределение с пятью степенями свободы. Корректировка заключается в повышении вероятности появления условий с малыми номерами.
; 
; 
;
.
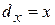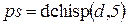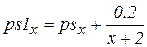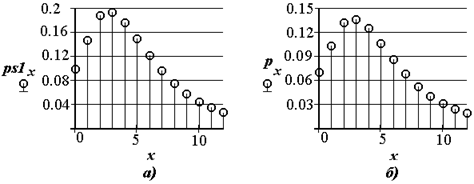
Рис. КСР.8. Функция распределения вероятности появления события номер x
Новая матрица индексных оценок принятия решений А1 приведена в табл. 5а.
Она дополнена столбцами наименьших, наибольших и средних (табл. 5б.). Оценки рассчитаны по формуле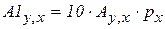 
. Коэффициент 10 введен искусственно. Он не влияет на процедуры принятия решений, но приближает цифры к оценкам последствий решений.
Таблица 5а
| Плата за решение при условии номер | ||||||||||||
| 1.7 | 5.7 | 1.1 | 3.5 | 8.4 | 2.6 | 2.4 | 5.3 | 2.2 | 1.3 | 2.7 | 1.5 | 0.7 |
| 3.5 | 4.3 | 0.6 | 7.2 | 7.3 | 1.5 | 4.6 | 4.9 | 1.3 | 2.1 | 2.6 | 0.9 | 1.0 |
| 4.4 | 2.3 | 2.5 | 9.5 | 4.7 | 2.1 | 6.3 | 3.6 | 1.2 | 3.0 | 2.1 | 0.6 | 1.4 |
| 3.9 | 0.9 | 5.8 | 9.2 | 2.4 | 4.3 | 6.6 | 2.0 | 2.0 | 3.3 | 1.3 | 0.8 | 1.6 |
| 2.5 | 1.3 | 8.7 | 6.8 | 1.9 | 6.8 | 5.3 | 1.3 | 3.2 | 2.9 | 0.7 | 1.3 | 1.5 |
| 1.1 | 3.4 | 9.6 | 3.7 | 3.6 | 8.0 | 3.3 | 1.7 | 4.0 | 2.0 | 0.7 | 1.8 | 1.1 |
| 0.7 | 5.8 | 8.0 | 2.0 | 6.4 | 7.3 | 1.7 | 3.1 | 4.0 | 1.0 | 1.2 | 1.9 | 0.6 |
| 1.5 | 7.3 | 5.0 | 2.6 | 8.7 | 5.1 | 1.4 | 4.5 | 3.0 | 0.6 | 1.8 | 1.6 | 0.3 |
| 3.1 | 7.0 | 2.3 | 5.2 | 9.0 | 2.6 | 2.6 | 5.0 | 1.7 | 0.9 | 2.2 | 0.9 | 0.3 |
| 4.5 | 5.0 | 1.6 | 8.2 | 7.1 | 1.3 | 4.5 | 4.3 | 0.7 | 1.7 | 2.1 | 0.4 | 0.6 |
Таблица 5б
| 0.7 | 8.4 | 3.0 |
| 0.6 | 7.3 | 3.2 |
| 0.6 | 9.5 | 3.3 |
| 0.8 | 9.2 | 3.4 |
| 0.7 | 8.6 | 3.5 |
| 0.7 | 9.6 | 3.4 |
| 0.6 | 8.0 | 3.4 |
| 0.3 | 8.7 | 3.3 |
| 0.3 | 9.0 | 3.3 |
| 0.4 | 8.2 | 3.2 |
В качестве этого коэффициента целесообразно брать число рассматриваемых условий реализации решений. В табл. 6 приведены результаты поиска оптимального решения по критерию Байеса–Лапласа.
Таблица 6
| Оценочная функция нейтральная, с вероятностью появления условия (критерий Байеса–Лапласа): | Номер решения | Индекс решения |
 .
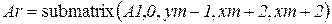Промежуточный массив для поиска max
 .
Номер решения, принятого по минимаксному критерию  ,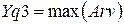
 .
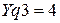| 3.0 | |
| 3.2 | ||
| 3.3 | ||
| 3.4 | ||
| 3.5 | ||
| 3.4 | ||
| 3.4 | ||
| 3.3 | ||
| 3.3 | ||
| 3.2 |
Дата добавления: 2015-03-23; просмотров: 700;