Графическое отображение поля выбора решения
Переработаем матрицу решения, оставив два условия осуществления решений. Одно из них определим, как усредненное из последствий условий с номерами 0-4, а условия с номерами 5-10 и 12 опустим. Данная процедура используется практически в каждом этапе итерации изложенной выше методики принятия решений. Мы проводим ее с предельным упрощением. Это обусловлено возможностями графического отображения функций на листе бумаги. Кроме того, сведение описаний ситуаций к двум вариантам в практике принятия решений человеком встречается часто.
Сформируем два столбца A2, A3. Первый, – как новое условие осуществления решения, объединяющее условия с номерами 0-5. Во второй перенесем условие с номером 11. Все компоненты умножим на 10, это необходимо для их использования в качестве адресов нового массива Z. Остальные опустим, как неучтенные. В полученных координатах поля выбора решений построим массив номеров решений, поднятый для наглядности на 10.
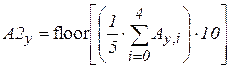 ;
;
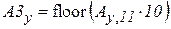 ;
;
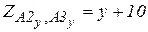 .
.
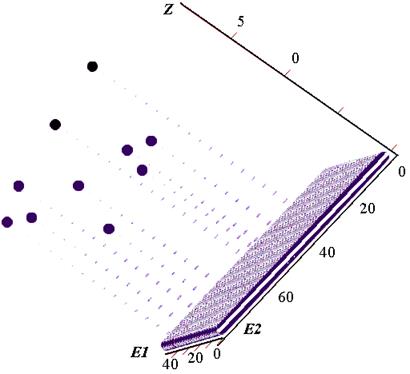
Рис. КСР.9. Решения на поле выбора решений
Потеряв номер решения (его можно в дальнейшем восстановить) изобразим следы решений на плоскости. Введем линии, ограничивающие поле выбора решений (вертикальные линии заданы как границы оси ординат).
Помещая рабочую точку в следы решений можно делать выбор, ориентируясь на геометрическую трактовку оценочных функций критериев принятия решений.
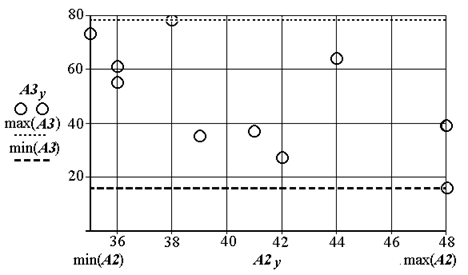
Рис. КСР.10. Поле выбора решения
Сформируем новую матрицу, введя столбцы А2, А3 и дополним ее min, max и mean по строке. В табл. 7 первый столбец – номер решения.
Таблица 7
| A2 | A3 | min | max | mean | |
| 48.5 | |||||
| 34.5 | |||||
| 45.5 | |||||
| 43.5 | |||||
Выберем критерий нейтрального игрока и найдем для сравнения номер решения по вышеописанной методике. Это решение номер 6.
Далее найдем решение по данному критерию, используя геометрические аналогии. Уравнение, определяющее вид линии предпочтения, в данном случае задает планируемый выигрыш, как величину B, пропорциональную сумме выигрышей по координатам B=S+i. Направляющая (N), вдоль которой движется линия предпочтения, является биссектрисой угла, образованного осями координат. Конус предпочтения движется в поле принятия решения до тех пор, пока в нем останется только одна точка.
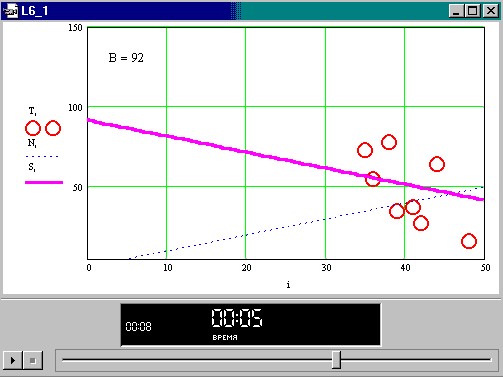
Рис. КСР.11. Конус предпочтения содержит три точки,
несущие больший выигрыш, чем рабочая
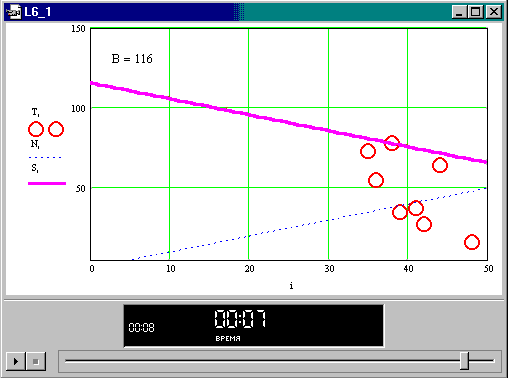
Рис. КСР.10. Все точки, кроме рабочей, вне конуса предпочтения
Эта точка соответствует оптимальному решению. На рисунках показаны кадры видеофильма, в котором смещается конус предпочтения.
Выбрано также решение номер 6 (78, 38).
Дата добавления: 2015-03-23; просмотров: 1115;
