Формирование матрицы решений

Учитывая опыт составления описания классов распознаваемых объектов, полученный в предыдущих работах, данный этап рекомендуется выполнить. В упрощенном примере, на базе которого поясняются этапы работы, элементы матрицы решения A генерируются. Они определены как сумма гармонической функции и функции Бесселя заданных в плоскости, координатами которой являются номер решения y и номер ситуации осуществления решения x (рис.КСР2.1).

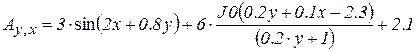Дополним матрицу столбцами min, max и mean, рассчитанными по строкам. Сформируем вектора X - строки из массива A и определим требуемое содержимое добавляемых столбцов.

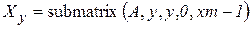где xm – число столбцов матрицы A.

;

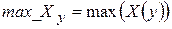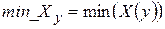Нарастим исходную матрицу строками и столбцами max, min и mean:

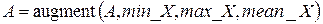Матрица представлена в табл. 1а и табл. 1б. Столбцы 13, 14, 15 – минимальное, максимальное, среднее значение результата решения, номер которого определяется номером строки.

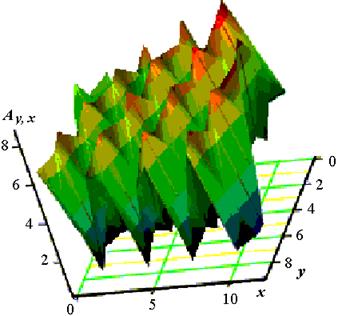
Рис. КСР. 7. Графическое представление матрицы решений

Таблица 1а

Плата за решение при условии

	2.4	0.8	5.4	2.6	6.7	2.5	2.8	7.8	3.2	4.3	8.5	6.1	3.7
	5.0	4.2	0.5	5.2	5.8	1.4	5.3	7.2	2.5	5.3	8.4	3.7	5.1
	6.3	2.2	1.9	6.9	3.7	2.0	7.3	5.3	2.3	7.4	6.7	2.7	7.2
	5.6	0.9	4.3	6.7	1.9	4.1	7.6	3.0	3.8	8.2	4.2	3.5	8.4
	3.6	1.3	6.5	5.0	1.5	6.4	6.2	1.9	6.0	7.2	2.4	5.5	7.9
	1.6	3.2	7.2	2.7	2.9	7.6	3.8	2.5	7.6	4.9	2.3	7.3	5.9
	1.0	5.6	6.0	1.4	5.1	6.9	1.9	4.5	7.5	2.6	3.8	7.8	3.3
	2.2	7.1	3.7	1.9	7.0	4.8	1.6	6.6	5.7	1.6	5.9	6.4	1.6
	4.4	6.7	1.7	3.8	7.2	2.4	3.0	7.4	3.2	2.3	7.2	3.9	1.7
	6.4	4.8	1.2	5.9	5.6	1.2	5.2	6.3	1.3	4.3	6.7	1.6	3.3

Таблица 1б

	Дополнительные столбцы

0.8	8.5	4.4
0.5	8.4	4.6
1.9	7.4	4.7
0.9	8.4	4.8
1.3	7.9	4.7
1.6	7.6	4.6
1.0	7.8	4.4
1.6	7.1	4.3
1.7	7.4	4.2
1.2	6.7	4.2

<16 17 181920 21 22 >

Дата добавления: 2015-03-23; просмотров: 806;