Пример 1.3.1.
Введение 3
Модуль I. Бытовая сфера общения. 1.1.Мy family.
1.2. Вводно-корректировочный фонетический курс 6
2.1. Ноuse.
2.2. Порядок слов в английском простом повествовательном предложении 9
3.1. Leisure time, family traveling
3.2. Личные и притяжательные местоимения 11
4.1. Shopping
4.2. Существительное 12
Модуль II. Учебно-познавательная сфера общения. 1.1. Higher education in Russia and abroad.
1.2. Степени сравнения прилагательных и наречий 17
2.1. My high school
2.2. Глагольные времена действительного залога (Simple Tenses) 19
3.1. Student's life in Russia and abroad.
3.2. Функции причастия I 24
4.1. Student's international contacts: scientific, professional, cultural.
4.2. Глагольные времена действительного залога (Continious Tenses) 25
Модуль III. Социально-культурная сфера общения. 1.1. Language as means of intercultural dialogue.
1.2. Глагольные времена действительного залога (Perfect Tenses)
2.1. National cultures.
2.2. Функции причастия II 28
3.1. International tourism.
3.2. Модальные глаголы и их эквиваленты 31
4.1. World achievements in art (music, dances, painting, theater, cinema, architecture)
4.2. Страдательный залог 33
5.1. Health, a healthy way of life, the nature world.
5.2. Независимый причастный оборот 34
6.1. Global problems of mankind and a way of their decision, information technologies of 21 centuries
6.2. Герундий 36
Модуль IV. Профессиональная сфера общения. 1.1. Selected direction of professional work
1.2. Инфинитив. Инфинитивные обороты. 38
2.1.History, perspectives of development of the modern science
2.2. Сослагательное наклонение 44
Рис. 1.3.3. График Еi-функции для 0,001 £ x £ 5,0
Разделение графиков Еi(x) и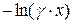 
на рис. 1.3.3 обосновано уравнением 1.3.5. Важность этого приближения заключается в том, что инженер-промысловик для анализа измеряет давление в скважине при r = rc. Теперь в случае, когда 
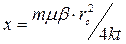, при обычных замерах в скважине можно определить, что х будет меньше, чем 0,01, даже для малых значений t.
Уравнение 1.3.2 может быть выражено как:
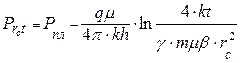. (1.3.6)
Таким образом, анализ полученных решений показывает [3], что решение на основе Ei-функции приближается к точному решению в интервале значений t :
.
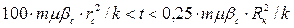Для времени меньшем, чем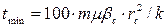 
, снижается точность решения уравнения (1.3.2), соответствующему ситуации, когда скважина имеет нулевой радиус и является линейным стоком. При времени, большем 
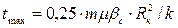влияние границ пласта становится ощутимым при расчете распределений давления в пласте и поэтому при времени большем этой величины далее нельзя рассматривать пласт как бесконечный резервуар.
Дальнейшее упрощение решения уравнения фильтрации возможно, если x < 0,02 и тогда Ei(-x)может быть аппроксимировано с точностью не менее 0,6 % функцией
Ei(-x)=ln (1,781 x). (1.3.7)
Функцию Ei(-x),значения которой приведены втаблице 1.3.1, следует применять при значениях аргумента x в пределах 0,02 < x < 10,9. Для x < 0,02 возможно применение аппроксимацию этой функции – уравнение (1.3.7). А, для x > 10,9функция Ei(-x)принимается равной нулю.
На практике замечено, что большинство скважин имеет пониженную проницаемость в призабойной (поврежденной) зоне, связанную с загрязнением пласта при бурении и во время работ по освоению скважины. Множество других скважин подвергаются кислотному воздействию или гидроразрывам пласта. Уравнение (1.3.2) отражает работу пласта при неизменной проницаемости во всей области пласта от скважины до бесконечности. Хавкинс [4] показал, что если в околоствольной зоне имеет место пониженная проницаемость, связанная с загрязнением пласта, или повышенная – вследствие интенсификации скважины, то такая зона с радиусом rs и проницаемостью ks может быть представлена как зона ПЗП, для преодоления сопротивления которой при движении жидкости к скважине требуется дополнительный перепад давления ∆Ps, который учитывается в уравнении (1.3.2) путем включения его как дополнительного члена (рис. 1.3.4).
Тогда уравнение (1.3.2) принимает вид:
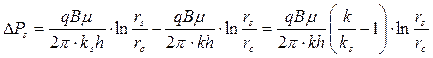, (1.3.8)
Уравнение (1.3.8) просто отражает тот факт, что перепад давления в ПЗП пропорционален проницаемости в призабойной зоне пласта ks и отличается от перепада давления в удаленной зоне с проницаемостью k.
Таблица 1.3.1
|
| х | ||||||||||
| 4,89 х 10-2 | 4,26 х 10-2 | 3,72 х 10-2 | 3,25 х 10-2 | 2,84 х 10-2 | 2,49 х 10-2 | 2,19 х 10-2 | 1,92 х 10-2 | 1,69 х 10-2 | 1,48 х 10-2 | |
| 1,30 х 10-2 | 1,15 х 10-2 | 1,01 х 10-2 | 8,94 х 10-3 | 7,89 х 10-3 | 6,87 х 10-3 | 6,16 х 10-3 | 5,45 х 10-3 | 4,82 х 10-3 | 4,27 х 10-2 | |
| 3,78 х 10-3 | 3,35 х 10-3 | 2,97 х 10-3 | 2,64 х 10-3 | 2,34 х 10-3 | 2,07 х 10-3 | 1,84 х 10-3 | 1,64 х 10-3 | 1,45 х 10-3 | 4,29 х 10-3 | |
| 1,15 х 10-3 | 1,02 х 10-3 | 9,08 х 10-4 | 8,09 х 10-4 | 7,19 х 10-4 | 6,41 х 10-4 | 5,71 х 10-4 | 5,09 х 10-4 | 4,53 х 10-4 | 4,04 х 10-4 | |
| 3,60 х 10-4 | 3,21 х 10-4 | 2,86 х 10-4 | 2,55 х 10-4 | 2,28 х 10-4 | 2,03 х 10-4 | 1,82 х 10-4 | 1,62 х 10-4 | 1,45 х 10-4 | 1,29 х 10-4 | |
| 1,15 х 10-4 | 1,03 х 10-4 | 9,22 х 10-5 | 8,24 х 10-5 | 7,36 х 10-5 | 6,58 х 10-5 | 5,89 х 10-5 | 5,26 х 10-5 | 4,71 х 10-5 | 4,21 х 10-5 | |
| 3,77 х 10-5 | 3,37 х 10-5 | 3,02 х 10-5 | 2,70 х 10-5 | 2,42 х 10-5 | 2,16 х 10-5 | 1,94 х 10-5 | 1,73 х 10-5 | 1,55 х 10-5 | 1,39 х 10-5 | |
| 1,24 х 10-5 | 1,11 х 10-5 | 9,99 х 10-6 | 8,95 х 10-6 | 8,02 х 10-6 | 7,18 х 10-6 | 6,44 х 10-6 | 5,77 х 10-6 | 5,17 х 10-6 | 4,64 х 10-6 | |
| 4,15 х 10-6 | 3,73 х 10-6 | 3,34 х 10-6 | 3,00 х 10-6 | 2,68 х 10-6 | 2,41 х 10-6 | 2,16 х 10-6 | 1,94 х 10-6 | 1,74 х 10-6 | 1,56 х 10-6 |
| |||
|
|
Рис. 1.3.4. Схема распределения давления в призабойной зоне пласта
Объединяя уравнения (1.3.2) и (1.3.8), находим, что суммарный перепад давления у скважины может быть представлен в виде:
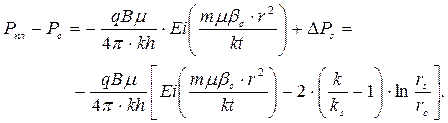
Для r = rс аргумент функции Ei становится достаточно малым сразу же после какого-то кратковременного периода работы скважины, поэтому возможно применение логарифмической аппроксимации функции Ei. Таким образом, процесс снижения давления в скважине после ее пуска в работу осуществляется в соответствии со следующим решением:
.
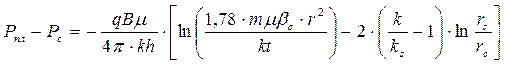Можно определить скин-фактор S, характеризующий состояние прискважинной зоны:
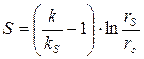. (1.3.9)
Таким образом, уравнение снижения давления после пуска скважины в работу с постоянным дебитом примет вид:
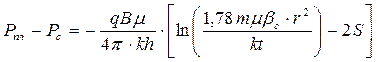. (1.3.10)
Уравнение (1.3.10) позволяет увидеть некоторый физический смысл скин-фактора по его знаку. Если скважина подвержена загрязнению, потери проницаемости в призабойной зоне (ks < k), то S положителен, и чем больше разница между ks и k, тем больше пласт подвержен повреждению и тем больше величина S. Нет ограничения сверху для S. Некоторые новые пробуренные скважины вообще не дают продукции нефти, пока не будет произведена интенсификация пласта; для таких скважин ks = 0 и S → ∞.
Если скважина интенсифицирована, когда в ней выполнена какая-то работа по воздействию на пласт (соляно-кислотная обработка, импульсное воздействие и т. д.), то пласт очищается и в призабойной зоне может оказаться проницаемость выше проницаемости пласта. Тогда ks > k и S становится отрицательным. Чем глубже пласт подвержен воздействию, тем больше будет численное значение скин-фактора. Реально, скважины, подверженные воздействию не могут иметь скин-фактор менее -7 или –8, и на практике высокие (отрицательные) скин-факторы могут возникнуть только при очень интенсивном глубоком воздействии на пласт, таком, например, как гидроразрыв пласта.
В конечном итоге можно сказать, что если скважина не подвержена загрязнению и не стимулирована, то ks = k и S = 0.
Заканчивая рассуждения о природе скин-фактора, заметим, что учитывать величину скин-фактора следует только в связи с определением изменения давления в призабойной зоне пласта. При изучении поведения давления в удаленной зоне пласта скин-фактор не принимается во внимание, так как изменение давления здесь определяется только свойствами пласта. Иными словами, уравнение (1.3.10) используется только при расчете давлений на стенке скважины и в призабойной зоне пласта, а уравнение (1.3.2) описывает изменение давления за пределами ПЗП, то есть во внешней области пласта на расстоянии r таком, что rс < r < Rк.
Пример 1.3.1.
Дата добавления: 2015-01-15; просмотров: 1081;