Рівняння теорії пластичності

Для незмінних властивостей тіла рівняння теорії пластичності базуються на рівняннях рівноваги (5.33), Коші (5.6) і умови пластичності (рівняння реології).

Для загального випадку навантаження тіло можна поділити на дві частини, в одній з яких діють тільки пружні деформації, а в іншій – пластичні. При цьому виникає необхідність визначення границі між цими частинами. Для одноосьового навантаження ця границя визначається границею текучості s_Т : при s<s_Т справедливий закон Гука, а при s³s_т використовують інші залежності між напруженнями і деформаціями. При плоскому або об’ємному напруженому стані застосовують критерії або умови пластичності (текучості), які є функцією інваріантів (5.2) тензора напружень.

Критерій Сен-Венана – Леві сформульований на припущенні, що пластичний стан настає при досягненні максимальних дотичних напружень границі текучості матеріалу і для об’ємного напруженого стану виражається формулою

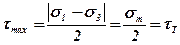, (5.37)

де t_Т –границя текучості матеріалу при зсуві.

Критерій Губера – Мізеса базується на припущенні, що пластичний стан настає при досягненні певного значення питомої пружної енергії деформації, характерної для даного матеріалу:

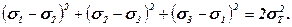(5.38)

Умова Губера – Мізеса для чистого зсуву

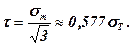
Досліди показують, що пластичні деформації при чистому зсуві виникають при t_т=(0,56…0,60)s_Т . Таким чином умова пластичності Губера – Мізеса дещо краще відповідає дослідним даним, ніж умова Сен-Венана – Леві. Втім, у теорії пластичності обидва критерії посідають рівноцінне місце. Їх вибір, як правило, визначається

Наведені критерії пластичності дозволяють визначити появу пластичних деформацій. Вони можуть бути використані як рівняння реології при розв’язанні задач пластичності для матеріалів, деформації яких при одноосьовому напруженому стані відповідає діаграмі Прандтля (рис. 5.7).

На даний час для ізотропних матеріалів запропоновано ряд співвідношень між напруженнями та деформаціями (рівняння реології), що використовуються в теорії пластичності. Їх поділяють на дві групи – деформаційні теорії пластичності та теорії пластичної течії.

У перших встановлюється взаємозв’язок між напруженнями в деформаціями, а в теоріях пластичної течії – між елементарними приростами пластичних деформацій і напруженнями.

Іншими словами, рівняння реології деформаційної теорії пластичності представлені кінцевими співвідношеннями між компонентами тензорів напружень і деформацій, а теорії пластичної течії – у вигляді диференціальних рівнянь.

Розглянемо для деформаційної теорії пластичності рівняння малих пружнопластичних деформацій, яка ґрунтується на наступних гіпотезах.

1 Об’ємна деформація тіла вважається пружною, тобто для об’ємної деформації справедливий закон Гука

,

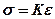де s – середнє напруження в точці;

e – об’ємна деформація;

К – об’ємний модуль пружності.

2. Девіатори напружень і деформацій збігаються з точністю до постійного множника c :

,

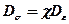або в скалярній формі

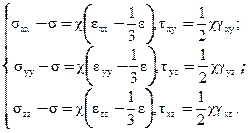(5.39)

Параметр c визначається із реологічних рівнянь (5.39)через інтенсивності нормальних напружень 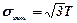та деформацій 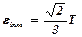(див. формули (5.5 і (5.9)):

.

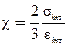3. Співвідношення 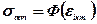не залежить від виду напруженого стану і задає реологічні рівняння (5.39) пружнопластичного матеріалу.

Теорія малих пружнопластичних деформацій справедлива в принципі тільки при простих навантаженнях. Експерименти показують, що і при складних навантаженнях, але близьких до простих, ця теорія дає задовільні результати.