Теорії міцності
Теорії міцності обґрунтовують можливість використання результатів модельних випробувань матеріалів на міцність при простих видах навантажень у розрахунках на міцність при складному напруженому стані.
Існує ряд теорій міцності, в основу яких покладені різні гіпотези руйнування матеріалу.
Перша теорія міцності ґрунтується на припущенні, що причиною руйнування матеріалу є відрив і він руйнується внаслідок досягнення напруженням граничного значення. Для складного напруженого стану (s1³s2³s3) умова міцності при s1>0 має вигляд
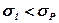 ,
,  (5.44)
(5.44)
де sР – міцність матеріалу на розтяг.
Досліди показують, що перша теорія міцності дає задовільні результати тільки при простих видах навантажень.
Друга теорія міцності також базується на припущенні, що матеріал руйнується в результаті відриву, але при досягненні деформації розтягу граничного значення. Умова міцності має вигляд
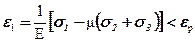
або через еквівалентні напруження
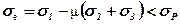 (5.45)
(5.45)
де eр– гранична деформація матеріалу в момент руйнування на розтяг.
Перша і друга теорії міцності є теоріями крихкого руйнування матеріалів. Друга теорія міцності не знайшла практичного застосування при складних напружених станах.
Третя теорія міцностіпобудована на гіпотезі, що матеріал руйнується внаслідок пластичних деформацій при досягненні максимальних дотичних напружень границі текучості (тобто зам критерієм Сен-Венана – Леві). Умова міцності для складного напруженого стану
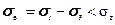 . (5.46)
. (5.46)
Четверта (енергетична) теорія міцності, як і третя, належить до теорії пластичного руйнування. Вважається, що матеріал руйнується при досягненні питомої енергії деформації граничного значення (критерій Губера – Мізеса). Умова міцності через еквівалентні напруження визначається за формулою
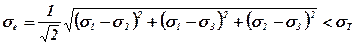 . (5.47)
. (5.47)
Теорії пластичного руйнування задовільно узгоджуються з експериментом для ізотропних матеріалів при складному напруженому стані і застосовуються на практиці.
Теорія міцності Мора враховує залежність граничного дотичного напруження ( 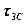 ) у момент руйнування матеріалу від середнього нормального напруження (s), тобто
) у момент руйнування матеріалу від середнього нормального напруження (s), тобто
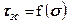 , (5.48)
, (5.48)
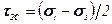 ;
; 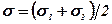 .
.
Побудова кривої (5.49) здійснюється на основі незалежних випробувань матеріалу, наприклад (рис. 5.9):
розтяг s1>0; s2=s3=0 (круг 1, sр – міцність на розтяг);
зсув s1= –s3; s2= 0;(круг 2, sЗС – міцність на зсув);
стиснення s1=s2=0; s3<0; (круг 2, sС – міцність на стиснення).
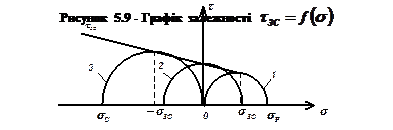 |
Огинаюча кругів Мора, побудованих за результатами випробувань відображає залежність (5.48), яку зазвичай апроксимують лінійною функцією
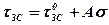 ,
,
де 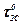 – граничне значення дотичних напружень при s=0;
– граничне значення дотичних напружень при s=0;
А – коефіцієнт внутрішнього тертя.
Узагальненням залежності (5.49) є умова виду
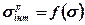 , (5.49)
, (5.49)
де 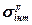 - гранична інтенсивність дотичних напружень у момент руйнування матеріалу;
- гранична інтенсивність дотичних напружень у момент руйнування матеріалу;
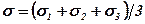 .
.
За результатами незалежних випробувань будують криві (5.48), (5.49).
Вважається, що найповнішою і найбільш наочною характеристикою міцності гірської породи в складному напруженому стані є огинаюча максимальних кругів Мора, або паспорт міцності.
Теорія міцності Гріффітса побудована на гіпотезі руйнування матеріалу шляхом розповсюдження тріщин, тобто дефектів матеріалу під дією навантажень. Вважається, що матеріал довільного тіла вміщує мікро тріщини, які під дією навантаження можуть збільшуватись і призводити до руйнування тіла або залишатись незмінними.
Розподіл мікротріщин в об’ємі тіла є випадковим, і тому значення міцності також випадкове Експериментально це переконливо підтверджується розсіюванням значень міцності при випробуваннях однакових зразків в одних і тих самих умовах та проявом так званого масштабного ефекту: більші зразки мають меншу міцність, ніж менші зразки такої ж форми. Це характерно для всіх крихких тіл, в тому числі і для гірських порід.
В основу критерію Гріффітса покладено припущення, що руйнування матеріалу відбувається, коли рівень напруженого стану поблизу вершини тріщини досягає граничного значення, що характеризує даний матеріал у відповідних умовах експлуатації (температура, швидкість навантаження і т. ін.). Формально умова міцності, або стійкості тріщини, оцінюється порівнянням значення коефіцієнта інтенсивності напружень Кінт із критичним Кс :
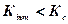 . (5.50)
. (5.50)
Значення Кінт визначається на основі розв’язку відповідних модельних задач теорії пружності для тіла з тріщиною. Наприклад, для простих випадків плоского і антиплоского напружених станів (рис. 5.10) Кінт визначається за формулами
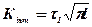 ;
; 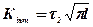 , (5.51)
, (5.51)

де s1, t1, t2 – відповідно нормальне та дотичні напруження.
Критичне значення коефіцієнта інтенсивності напружень визначають з досліду при відомій довжині тріщини для відповідної схеми навантаження за формулами типу (5.51).
Умова (5.50) з оцінками формул (5.51) відображає міцність крихкого руйнування матеріалу.
Відомо їх узагальнення на випадок пружнопластичного напруженого стану, в тому числі і побудова так званих діаграм оцінки руйнувань за критеріями крихкого і пластичного руйнування матеріалу.
Дата добавления: 2015-03-20; просмотров: 1885;
