Міцнісні властивості

Міцність– це здатність порід чинити опір руйнуванню під дією прикладених механічних напружень.

Вона характеризується межею міцності при стиску і розтягу, зчепленням і кутом внутрішнього тертя.

Межею міцностіs називають напруження, при якому зразок руйнується:

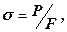(6.7)

де P – руйнівне навантаження;

F – площа, на яку діє прикладене навантаження.

Межа міцності при одноосьовому стиску зразків гірських порід, або коротше міцність на стиск s_ст – найуживаніша характеристика міцності порід. Її най­більші значення для порід досягають 500 МПа (найміцнішими є базальти і кварцити), мінімальні значення вимірюються одиницями і навіть десятими частками МПа (мергель, гіпс, кам’яна сіль, насичена водою). Залежно від складу і структури порід навіть однієї петрографічної назви міцність на стиск може змінюватись у широких межах. Так, показник s_ст для різних базальтів змінюється в діапазоні (30÷500) МПа, гранітів (37÷380) МПа . Зазвичай міцність порід на стиск тим більша, чим більша їх густина.

Міцність на розтяг s_р гірських порід значно менша за міцність на стиск. Ця особливість характерна лише для гірських порід і визначає їх поведінку в полі механічних сил. Дійсно, для сталі і ряду інших матеріалів показники s_ст і s_р , як відомо, рівні між собою. Гірські породи ж погано протистоять зусиллям розтягу, поява яких в тих чи інших ділянках масиву виробок є критерієм небезпеки обвалювання порід і руйнування гірничих виробок. Пояснити таку особливість гірських порід можна наступним чином: через специфіку внутрішньої будови стискуючим зусиллям противиться увесь матеріал породи, а при розтягу зразка руйнування відбувається в найслабших місцях з’єднання мінеральних зерен.

Відношення s_р/s_ст є вельми показовим для порівняльної характеристики різних порід. В механіці гірських порід його звичайно визначають у вигляді простого дробу з одиницею в чисельнику. Це співвідношення для різних порід коливається в межах 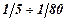, найчастіше в межах 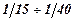. Верхня межа відповідає глинистим породам, нижня – найбільш крихким породам (гранітам, пісковикам та ін.).

Міцність на зріз (зсув) характеризується двома функціонально пов’я­заними параметрами: зчепленням і кутом внутрішнього тертя породи. Цей функціональний зв’язок відомий як рівняння Кулона:

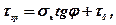(6.8)

де t _зр – напруження зрізу;

s_н – нормальне напруження при зрізі;

j – кут внутрішнього тертя;

t₀ – зчеплення.

Зчепленняt₀ характеризує граничний опір зрізу по площадці, на якій немає нормального тиску, тобто немає опору зрізним зусиллям за рахунок внутрішнього тертя.

Кут внутрішнього тертяj або коефіцієнт внутрішнього тертяtg j характеризує інтенсивність збільшення зрізних зусиль із збільшенням нормальних напружень, тобто є коефіцієнтом пропорційності між приростом дотичних dt_nі нормальних ds_n напружень при зрізі:

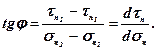(6.9)

Значення зчеплення гірських порід змінюється в межах від сотих часток (глини, мергелі, слабо зцементовані пісковики та ін.) до десятків МПа (міцні пісковики і масивно-кристалічні породи), кут внутрішнього тертя – від 10­¸15 для деяких глин до 35¸40 для міцних масивно-кристалічних і метаморфічних порід (граніти, сієніти, кварцити та ін.) і грубозернистих сипучих порід (гальковики, грубозернисті піски та ін.).

Деформаційні властивості характеризують поведінку твердого тіла під дією зовнішніх сил до моменту його руйнування. До них належать пружні, пластичні властивості а також така характеристика гірських порід як повзучість.

Пружні властивості гірських порід характеризуються модулем пружності Е при одноосьовому напруженому стані (модулем поздовжньої пружності або, інакше, модулем Юнга), модулем зсуву G, модулем об’ємної пружності К і коефіцієнтом поперечних деформацій m (коефіцієнтом Пуассона).

Модуль пружностіЕ – це відношення нормальних напружень s_n до відносної лінійної деформації зразка e_l=Dl/l в напрямі дії прикладеного навантаження:

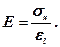(6.10)

Модуль зсувуG – це відношення дотичного напруження t до відносного зсуву q :

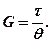(6.11)

Відносний зсув ще інколи називають кутовою деформацією. Він характеризує зміну форми тіла, що деформується, і визначається із залежності:

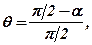(6.12)

де a – кут нахилу кожного прямокутного елементу тіла після його деформування.

Об’ємний модуль пружностіК, або модуль усестороннього стиску – це відношення рівномірного усестороннього напруження до відносної пружної зміни об’єму зразка:

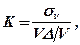(6.13)

де 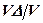– відносна пружна зміна об’єму.

Коефіцієнт поперечних деформацій μ, або коефіцієнт Пуассона є мірою пропорційності між відносними деформаціями в напрямку, перпендикулярному до вектора прикладеного навантаження і паралельному йому:

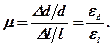(6.14)

Перелічені характеристики пружних властивостей функціонально зв’язані між собою такими співвідношеннями:

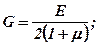(6.15)

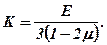(6.16)

Таким чином, знаючи дві з чотирьох характеристик, можна розрахунковим шляхом визначити значення інших. Зазвичай на зразках порід експериментально визначають характеристики Е і μ, а величини G і К розраховують.

Модулі пружності порід змінюються в межах (1¸3)·10³–(1¸3)·10⁵ МПа. Найменші значення модуля пружності мають пористі туфи, слабкі глинисті сланці, галіт, гнейси, філіти, а найбільші – у базальтів, діабазів, піроксенітів, дунітів, монтичеліту. Із збільшенням густини порід їх модуль пружності, як правило, збільшується. Модуль пружності шаруватих порід в напрямку шаруватості більший, чим перпендикулярно до нашарування.

Коефіцієнт поперечних деформацій μ гірських порід теоретично може змінюватися в межах від 0 до 0,5.

Для більшості порід його значення коливаються в інтервалі значень від 0,15 до 0,35. Мінімальні значення μ мають деякі біотитові і вапнисті сланці, опал, філіти, гнейси (0,01÷0,08), максимальні – деякі дуніти, амфіболіти (0,40÷0,46).

Для реальних пружних твердих тіл закон Гука справджується лише приблизно. Зокрема, модуль деформації при навантаженні дещо менший чим при розвантаженні, що у випадку швидкого зняття навантаження зумовлює залишкову деформацію е_зал ( рис. 4, а). Це явище називають пружним гістерезисом. Однак, з часом набута таким чином залишкова деформація зникає і тверде тіло відновлює свої розміри (рис. 4, б). Це явище називають пружною післядією.

Явища пружного гістерезисну і пружної післядії вказують на те, що деформації з часом можуть змінюватися.

До деякої величини напруження породи, яку називають межею пружності залишкові напруження при короткочасному навантаженні в ній практично не проявляються; деформації мають чисто пружний характер і при знятті навантаження зникають. Якщо ж значення напружень більші за межу пружності, то наряду з пружними деформаціями виникають і пластичні, котрі зберігаються і після розвантаження породи.

Пластичні властивості можна охарактеризувати коефіцієнтом пластичності, який є відношенням роботи А_р, витраченої на руйнування певного об’єму реальної гірської породи до роботи А_пр, потрібної для руйнування такого ж об’єму породи, з тим же значенням межі міцності при стиску при умові ідеальної пружності породи:

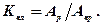(6.17)

Реологічні властивості

Механічні характеристики гірських порід визначають зазвичай при короткочасному прикладенні навантаження. Однак, гірничі виробки, елементи систем розробки, бурові свердловини сприймають навантаження протягом багатьох років.

Питаннями поведінки матеріалів, в т.ч. і гірських порід, в умовах тривалих силових навантажень займається реологія – наука про течію речовини.

Залежно від зовнішніх умов зміна напружено-деформованого стану твердого тіла в часі може відбуватися двома шляхами.

Наприклад, навантажимо зразок гірської породи, який має форму циліндра, деяким постійним неруйнівним навантаженням. Це практично миттєво спричинить певну відносну деформацію, величина якої залежить від прикладеного навантаження і модуля пружності матеріалу. Надалі при незмінному напруженні деформація не залишатиметься постійною, як це випливає із закону Гука. Її величина буде монотонно збільшуватися.

Повзучістю називається реологічне явище, яке полягає в тому, що з плином часу при постійному напруженні деформації зростають.

В другому випадку стиснемо зразок між двома плитами пресу так, щоб протягом усього досліду відстань між ними була строго фіксованою, тобто незмінною в часі. Почнемо вимірювати тиск на плити преса з боку зразка і переконаємося, що з часом його величина буде зменшуватися.

Реологічне явище, коли з плином часу при постійних деформаціях напруження зменшуються називають релаксацією напружень.

Повзучість гірських порід не є постійною величиною. Швидкість повзучості з часом змінюється. На рис. 6.2 подано типову залежність деформації повзучості від часу при постійному навантаженні і температурі. За зміною швидкості повзучості розрізняють три періоди.

Протягом першого періоду спостерігається зменшення швидкості повзучості – неусталена повзучість. Протягом другого періоду швидкість повзучості залишається постійною – усталена повзучість. В третьому періоді швидкість повзучості, як правило, зростає і деформація закінчується руйнуванням твердого тіла.

Міцність і пружність порід при тривалій дії достатньо великих навантажень зменшуються, асимптотично наближаючись до деяких граничних значень – границі тривалої міцності σ_¥ і граничного модуля тривалої пружності Е_¥. Для більшості порід σ_¥ = (0,7¸0,8) σ, Е_¥. = (0,65¸0,95) Е.

Завдання реології полягає в тому, щоб описати напружено-деформований стан гірських порід та інших матеріалів з урахуванням їх схильності до повзучості і релаксації. Воно зводиться до складення так званих рівнянь стану, які зв’язують в єдині співвідношення компоненти напружень, деформацій та їх похідних в часі.

В усіх наявних дослідженнях припускається, що рівняння стану достатньо точно описують зміни напружено-дефор-мованого стану матеріалів у тому випадку, коли зовнішні умови такі, що ні деформації, ні напруження не можна вважати постійними. Для наочності відображення реологічних процесів використовують властивості тіла описуються за

допомогою певним чином підібраної механічної моделі. Модель повинна складатися з елементів, які ідеально відображають основні фундаментальні властивості вихідного матеріалу.

Так, наприклад, при певному рівні навантажень і достатньо швидкому їх прикладенні усі тверді зв’язані гірські породи поводять себе як пружні тіла, що підлягають закону пружності Гука. Ця властивість твердих тіл моделюється елементом Гука − пружиною, жорсткість якої пропорційна модулю пружності (рис. 6.3, а). Пружні властивості твердих тіл не залежать від часу:

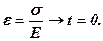(6.18)

Спеціальними дослідженнями встановлено, що границі зерен в полікристалічних матеріалах, до яких відносяться і гірські породи, поводять себе як в’язка рідина. Ця обставина приводить до того, що температура суттєво змінює внутрішнє тертя в таких тілах, їх міцнісні і деформаційні характеристики. В умовах достатньо тривалих зовнішніх навантажень полікристалічні матеріали поводять себе в цілому як в’язка рідина.

В’язкі властивості матеріалів моделює елемент Ньютона (рис. 6.3, б), який має вид демпфера-циліндра з отворами, зануреного у в’язку рідину.

Швидкість деформування в цьому випадку пропорційна діючим напруженням

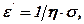(6.19)

де η – коефіцієнт в’язкості,

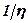– коефіцієнт текучості

При заданому постійному напруженні повна деформація до моменту часу t складе 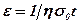, а при змінних в часі напруженнях .

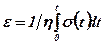При достатньо великих навантаженнях в гірських породах починається руйнування внутрішніх зв’язків, що призводить до утворення незворотних (пластичних) деформацій. Цю властивість реальних твердих тіл відображає елемент Сен-Венана. Він є елементом сухого тертя: брусок, що лежить на жорсткій поверхні (рис. 6.3, в). При навантаженні, меншому за деяку величину σ_т , деформація дорівнює нулю, при більшому – деформація невизначена: система починає рухатися і брусок залишається там, де припинилася дія сили.

Таким чином, розглянуті елементарні механічні моделі мають визначену фізичну основу.

З’єднуючи структурні елементи один з одним тим чи іншим способом, створюють складніші моделі, які в більшій мірі відображають властивості реальних матеріалів. Схеми з’єднання цих елементів визначені лише за формальною відповідністю властивостей складеної моделі властивостям реальних тіл. Однією з перших простих структурних механічних моделей твердого тіла є модель, запропонована Максвеллом. Вона складається із послідовно зв’язаних в’язкого і пружного елементів (рис. 6.4).

Навантаження, прикладене до системи, спричинює миттєву пружну деформацію пружини, що відповідає закону Гука. Надалі деформація системи зростає в часі з постійною швидкістю за рахунок в’язкого елемента. При знятті навантаження модель отримає зворотну деформацію, котра дорівнює початковій пружній. В’язка складова деформації незворотна.

Якщо моделі надати постійну деформацію, то поршень буде рухатися вгору до того часу, поки натяг пружини не зменшиться до нуля і вся пружна деформація перейде у в’язку. Це явище відповідає релаксації напружень.

Повзучість деформацій в середовищі Максвелла характеризується лінійним законом, релаксація напружень – експоненціальним:

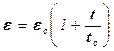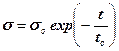; . (6.20)

Постійна величина t₀ називається періодом релаксації і, як випливає з формули (6.20) дорівнює часу, за який напруження зменшуються в еразів, е – основа натурального логарифма.

Слід зазначити, що модель Максвелла лише якісно відображає властивості реальних гірських порід, кількісні ж результати погано узгоджуються з експериментальними даними.

Ще одним важливим показником властивостей гірських порід є їх крихкість – здатність порід руйнуватися від прикладених навантажень без суттєвої залишкової (пластичної) деформації.

Крихкість характеризують коефіцієнтом крихкості, який є відношенням роботи, затраченої на деформування зразка до межі пружності А_пр, до загальної роботи А_р, потрібної для руйнування цього зразка:

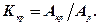(6.21)

Значення K_кр для різних порід змінюється в доволі широких межах. Наприклад, для вапняків і мармуру K_кр = 0,06¸0,07, а для йоліт-уртиту K_кр = 0,54.

У крихких тіл межа міцності наближається до межі пружності. Прояв крихкості гірських порід суттєво залежить від тривалості дії сили. Динамічні, ударні навантаження спричинюють крихке руйнування породи, тоді як тривала дія навіть порівняно невеликих навантажень може призвести лише до пластичних деформацій.

Специфічною характеристикою, котра іноді використовується в механіці гірських порід є розпушуваність – здатність гірської породи займати в розпушеному стані більший об’єм порівняно з тим, який вона займала в масиві.

Показником розпушуваності є коефіцієнт розпушеності K_р – відношення об’єму V_р породи після її розпушення при руйнуванні до об’єму V_м в масиві, тобто до розпушування:

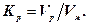(6.22)

Найменше розпушуються при інших рівних умовах піщані і глинисті породи (K_р=1,15¸1,20), найбільше – крихкі скельні породи (K_р=1,30¸1,40).З часом розпушені породи ущільнюються, однак і після ущільнення вони не досягають початкової щільності в масиві, яка була до розпушування.

Акустичні властивості

Визначають умови розповсюдження в гірських породах пружних коливань. Вони характеризуються швидкістю розповсюдження пружних хвиль v, акустичним опором Q і коефіцієнтом поглинання α.

Серед різних пружних коливань в твердих тілах найбільший інтерес становлять поздовжні, поперечні і поверхневі (релеєвські) хвилі. В поздовжніх хвилях напрям коливання частинок породи співпадає з напрямом розповсюдження хвилі; в поперечних напрям коливання частин перпендикулярно до напряму розповсюдження хвилі. Поверхневі хвилі – це коливання поверхні середовища (поверхні зразка гірської породи).

Співвідношення між швидкостями поздовжніх v_P, поперечних v_S і поверхневихv_R пружних хвиль характеризується такою нерівністю:

v_Р >v_S >v_R (23)

Швидкості розповсюдження пружних хвиль визначаються густиною і показниками пружності середовища. Густина характеризує масу, що зміщується, показники пружності – сили, котрі виникають із зміщенням частин, які коливаються. Теоретичний взаємозв’язок цих швидкостей з деформаційними характеристиками і густиною середовища визначається наступними залежностями:

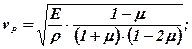(6.24)

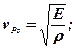(6.25)

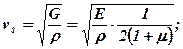(6.26)

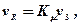(6.27)

де v_P – швидкість поздовжньої хвилі в необмеженому середовищі,

v_Pс – швидкість поздовжньої хвилі в стержні;

К_µ – безрозмірний коефіцієнт, що залежить від коефіцієнта поперечних деформацій (при μ=0,25К_v=0,9194, при μ=0,5К_v=0,9553).

Акустичним опором або акустичною жорсткістю називають добуток густини гірської породи на швидкість відповідної хвилі:

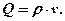(6.28)

Він характеризує вплив властивостей середовища на інтенсивність (частоту) коливань в цьому середовищі І, яка, крім того, визначається ще й параметрами збудника коливань.

Оскільки гірські породи не є ідеально пружними твердими тілами, в них через поглинання енергії коливань внаслідок тертя теплопровідності та інших ефектів пружні хвилі затухають. Це послаблення або затухання підлягає закону експоненти і описується такими виразами:

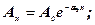(6.29)

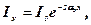(6.30)

де А₀ та І₀ – початкові амплітуда та інтенсивність коливань;

А_х та І_х –амплітуда та інтенсивність коливань після проходження хвилею в середовищі відстані х;

α_з – амплітудний коефіцієнт затухання.

Швидкість поздовжніх пружних хвиль є найуживанішою характеристикою. Її значення для різних вивержених порід змінюються в межах 3,5÷7,0 км/с, досягаючи інколи до 8,5 км/с осадових породах вона дещо менша і складає 1,5÷4,5 км/с і лише в щільних вапняках досягає 6÷7 км/с неконсолідованих уламкових і незцементованих уламкових товщах вона ще менша (0,1÷2,0 км/с) .

Із зростанням стискуючих зусиль швидкості пружних хвиль в гірських породах зростають.