В'язко-пружні властивості біологічних тканин
Біологічні структури (м'язи, судини, сухожилля, тканини легенів, шкіра тощо) являють собою в'язко-пружні системи, їх поведінка вивчається на моделях, що вміщують пружні (Е) та в'язкі (η) елементи, у деяких випадках до них додають і елементи зовнішнього тертя (К).
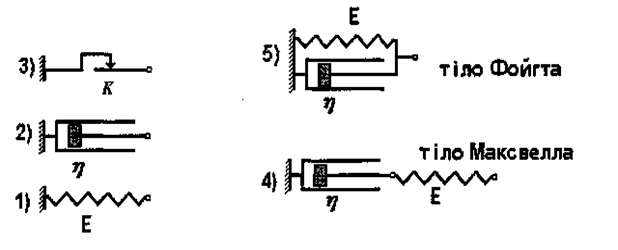
Мал. 1.10. Механічні моделі тканин: 1) пружний елемент; 2) в'язкий елемент; 3) елемент внутрішнього тертя; 4) послідовне з'єднання в'язкого та пружного елементів; 5) паралельне з'єднання в'язкого та пружного елементів.
Пружний елемент являє собою ідеальну пружину, для якої виконується закон Гука. В'язкий елемент може бути поданий у вигляді циліндра, який заповнений в'язкою рідиною з нещільним поршнем. Для витягування поршня необхідно прикласти деяку зовнішню силу, яка компенсує сили в'язкого тертя, що виникають при плині рідини крізь зазор.
Напруження, що створюються цими елементами під дією зовнішніх сил, дорівнюють:
· 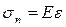 для пружного елементу;
для пружного елементу;
· 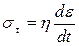 для в’язкого елементу;
для в’язкого елементу;
·  ~ KFn для елементу зовнішнього тертя при силі нормального тиску Fn і коефіцієнті тертя К.
~ KFn для елементу зовнішнього тертя при силі нормального тиску Fn і коефіцієнті тертя К.
Для відтворення механічних властивостей біологічних тканин використовують моделі, що складаються з цих елементів. Найпростішими моделями є тіло Максвелла і тіло Фойгта, що являють собою послідовне і паралельне з'єднання пружного та в'язкого елементів (див. мал. 1.10). Ці моделі дозволяють відтворити такі динамічні властивості тканин, як повзучість та релаксація напруження.
Повзучість - це явище зміни з часом розмірів зразка в умовах дії постійного напруження. Якщо у біологічних тканинах швидко створити, а потім підтримувати постійним деяке напруження, то з часом відбувається поступове подовження зразка аж до розриву тканин, навіть при умові, що постійне напруження має менше значення, ніж межа міцності матеріалу. Динаміку повзучості подано на мал. 1.1 la. Зміна розмірів відбувається тим швидше, чим більше напруження, що підтримується у зразку (порівняйте криві 1, 2 та 3, для яких (σ1 > σ2 > σ3).
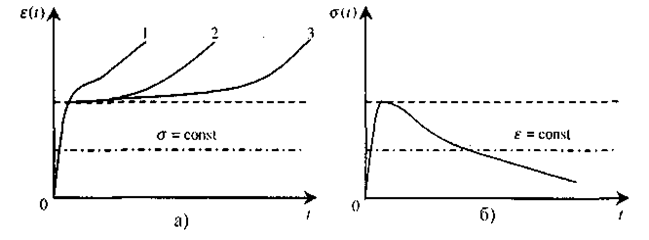
Мал. 1.11. Динамічні властивості біологічних тканин: а) повзучість - зміна деформації тіла за умови постійного напруження σ (σ1 > σ2 > σ3); б) релаксація напруження - зменшення σ в умовах постійної деформації.
Релаксація напруження - явище зменшення з часом величини напруження у зразку при підтримці постійної величини деформації. Якщо швидко розтягнути зразок і, підтримуючи постійною отриману деформацію, вимірювати напруження в ньому протягом деякого часу, помітним стане його зменшення з часом (мал. 1.116). Пунктирними лініями на обох мал. 1.11 відтворено поведінку чисто пружних тіл. Релаксація напруження і повзучість суто динамічні процеси - час їх існування вимірюється секундами або хвилинами. Наприклад, для м'язів час зменшення напруження на 40% становить близько 10 секунд.
Ці процеси легко пояснюються механічними моделями, наведеними на мал. 1.10 (позиція 4). Спочатку під дією зовнішніх сил деформується пружний елемент, а потім починається "плин" в'язкого елементу, змінюється його розмір, що викликає зміну як довжини, так і напруження. За допомогою моделі Максвелла легко отримати експоненціальний закон релаксації напруження
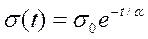 , (1.13)
, (1.13)
де α- постійна часу релаксації, σ0 = Еε- початкове напруження.
Явище повзучості також можна описати експоненціальним законом
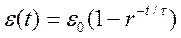 (1.14)
(1.14)
де ε0= σ0/Е - початкова деформація, τ- характерний час процесу повзучості, що дорівнює відношенню коефіцієнта в'язкості і модуля Юнга. Формулу τ= η/Е легко отримати з міркувань розмірності. Дійсно, розмірність η є Па*с, a розмірність Е дорівнює Н/м2 = Па. Тому єдина комбінація величин ηі Е, що має розмірність часу [τ] = с, є їх відношення η/е.
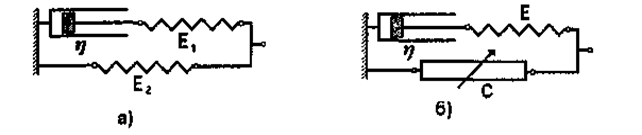
Мал. 1.12. Приклади механічних моделей біологічних тканин: а) трьохелементна модель для дослідження механічних властивостей 1в'язко-пружних тканин; б) трьохелементна модель м'язів, що включає скорочувальний елемент С.
Модель Фойгта дозволяє пояснити поступове зростання з часом напруження у зразку, якщо до тіла прикласти зусилля, що змінюється стрибкоподібне. Динаміка експоненціального зменшення напруження чи деформації відрізняється від експерименту. Кращих результатів можна досягти, якщо розглядати моделі, що включають до себе кілька пружних та в'язких елементів. Приклад однієї з таких моделей наведено на мал. 1.12. На цьому ж малюнку наведено одну з найпростіших моделей м'язів, що включає скорочувальний елемент С, котрий являє собою механохімічний конвертор, який перетворює енергію хімічних реакцій на механічну енергію. Ця механічна енергія витрачається на створення напруження і здійснення роботи по скороченню м'язів.
Наявність в'язко-пружних елементів, з'єднаних зі скорочувальними елементами, забезпечують ті гнучкі функціональні властивості, які притаманні цілому ряду фізіологічних систем (наприклад, серцево-судинній, м'язовій і ряду інших) для виконання призначених їм функцій в умовах зміни як властивостей самої системи, так і зовнішних навантажень. Це явище притаманне системам, які адаптуються. Так, зміна тонусу судин еласто-м'язового типу дозволяє реалізувати таке явище, як депонування крові, при якому значне збільшення об'єму судини можливе лише при повній релаксації стінки судини і зменшенні її пружності. Навпаки, при необхідності вигнання крові з депо об'єм судин зменшується, релаксація напруження
відбувається при інших розмірах судини, у цьому випадку зростає і модуль об'ємної пружності судин (їх тонус).
Дата добавления: 2015-03-03; просмотров: 3620;
