Основні поняття теорії фільтрації

При бурінні відбувається масообмін між свердловиною і розкритими пластами, кий визначається фільтраційними, дифузійними, осмотичними та іншими процесами. Фільтрація належить до найбільш вагомих процесів, що впливають на виникнення ускладнень при бурінні і кріпленні свердловин, ефективність розкриття і освоєння продуктивних горизонтів тощо.

Пустоти пористого середовища можуть заповнюватися різними фазами – нафтою, водою, газом.

Насиченість порового простору гірської породи характеризується коефіцієнтами насиченості нафтою S_н, водою S_в, газом S_г, які визначаються відношенням об’єму пор зайнятих відповідною фазою, до загального об’єму пор.

Рух рідин або газу в пористих породах внаслідок перепаду тиску називають фільтрацією. Потік рідини або газу в пористому середовищі характеризується об’ємною Q або масовою G витратою. Відношення об’ємної витрати рідини або газу через гірську породу до площі фільтрації F називається швидкістю фільтрації:

.

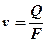За площу фільтрації приймається площа поверхні пористого середовища, нормально орієнтована відносно напрямку фільтрації.

До площі фільтрації належить як площа пустот, так і площа твердої фази (скелета) пористого середовища, тому що швидкість фільтрації є умовна (фіктивна) величина, що введена для зручності аналізу процесів руху в пористому середовищі. Дійсна (істинна) швидкість фільтрації v_д пов’язана з фіктивною швидкістю v співвідношенням

,

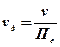де П_е – ефективна пористість породи.

Закони фільтрації виражають зв’язок між швидкістю фільтрації і умовами, в яких вона відбувається . З позиції нафтогазової механіки закони фільтрації акумулюють рівняння руху та реології і мають фундаментальний характер.

Закон фільтрації Дарсі, або лінійний закон фільтрації, установлений експериментально і узагальнений в диференціальній формі

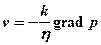, (5.52)

де v – вектор швидкості фільтрації;

k – коефіцієнт проникності пористого середовища;

h – в’язкість рідини або газу;

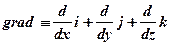– операція градієнта;

де i, j, k – одиничні орти декартової системи координат.

Коефіцієнт проникності характеризує здатність пористої гірської породи пропускати через себе рідину або газ при створенні перепаду тиску і має розмірність площі (м²). Коефіцієнт проникності залежить також від природи флюїду та умов фільтрації, що зумовлено фізико-хімічною взаємодією скелета пористого середовища з активними компонентами флюїду. Для характеристики тільки пористого середовища використовують коефіцієнт абсолютної проникності , який вимірюється при фільтрації інертних по відношенню до скелета породи рідини або газу. Проникність гірських порід-колекторів змінюється у широких межах – від тисячних часток до одиниць мкм² (1 мкм² =10^{-12 м2}).

Закон Дарсі ефективно діє при відносно малих швидкостях фільтрації, коли втрати тиску пов’язані лише з внутрішнім тертям.

Закон фільтрації Форхгеймера, або двочленний закон фільтрації, в диференціальній формі записується у вигляді

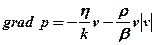, (5.53)

де r – густина рідини або газу;

b– коефіцієнт структури порового простору.

Коефіцієнт структури порового простору, як і коефіцієнт проникності, визначається дослідним шляхом і характеризує інерційну складову втрат тиску при фільтрації.

Закон фільтрації Форхгеймера є більш загальним у порівнянні із законом Дарсі. Для малих швидкостей фільтрації або великих значень параметра b частка другої складової у формулі (5.53) незначна, і градієнт тиску залежатиме, в основному, від сил тертя, тобто закон Дарсі буде справедливим.

Закони фільтрації Дарсі і Форхгеймера одержані для ньютонівської (в’язкої) рідини або газу. Порушення лінійного закону фільтрації може бути пов’язане і з аномальними реологічними властивостями рідини.

Закон фільтрації з початковим градієнтом зсуву відображає фільтрацію в’язко-пластичної рідини:

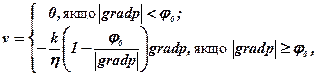(5.54)

де j₀ – початковий градієнт зсуву.

Значення початкового градієнта зсуву для одновимірної фільтрації може бути оцінене за формулою

,

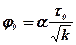де t₀ – динамічне напруження зсуву рідини;

a – емпіричний коефіцієнт (для пісківa=0,015 –0,018 ).

Закон Дарсі узагальнюють також на випадок багатофазової течії у пористому середовищі. Для цього розповсюджують поняття швидкості фільтрації на окрему фазу v_i , як відношення об’ємної витрати цієї фази Q_і до загальної площі фільтрації

.

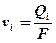Пропускна здатність пористого середовища для конкретної фази визначається коефіцієнтом відносної фазової проникності

,

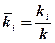де 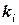– коефіцієнт проникності і-ї фази.

Закон фільтрації Дарсі для кожної фази записується у вигляді

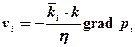. (5.55)

У загальному випадку градієнти тиску 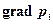у фазах за рахунок капілярного тиску різні, однак цією різницею часто нехтують і тиски у фазах приймають однаковими.

Коефіцієнти фазових проникностей залежать від насиченості пористого середовища. На рис. 5.11 показані криві відносних фазових проникностей для нафти і води при їх сумісній фільтрації. Аналогічні залежності спостерігаються також при інших випадках двофазової сумісної фільтрації.

 

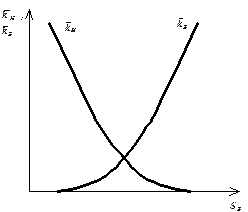Рисунок 5.11 – Криві відносних фазових проникностей для нафти ( 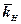) і води ( 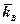) при їх сумісній фільтраціїї

 

Залежності фазових проникностей від насиченості пористого середовища можуть бути встановлені тільки дослідним шляхом для відповідних умов фільтрації.

Основними характерними ознаками задач фільтрації рідин та газів у пластах є кількість фаз, кількість компонентів та розмірність системи просторових координат. Якщо модель враховує рух лише однієї фази, то її називають однофазовою, а в протилежному випадку – багатофазовою. Якщо хоча б одна з фаз складається з двох або більше компонентів, то така модель є багатокомпонентною, в протилежному випадку – однокомпонентною. За розмірністю просторової системи координат розрізняють одно -, дво - і тривимірні задачі фільтрації.

Формулювання моделей фільтрації рідин або газів в пластах у загальному випадку містить закон фільтрації, рівняння збереження маси, рівняння стану та граничні і початкові (для неусталеної фільтрації) умови.

Рівняння збереження маси,або неперервності, записують у вигляді

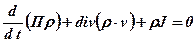, (5.56)

де П – пористість пласта;

J – об’ємна інтенсивність можливих джерел або стоків речовини (наприклад, свердловин).

При відсутності стоків або джерел рівняння неперервності набуває вигляду:

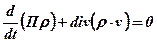, (5.57)

а для нестисливих рідин і скелета пористого середовища ( )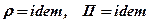

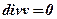. (5.58)

Рівняння стану, так само як у механіці суцільних середовищ, відображають залежність фізичних величин, що входять у закон фільтрації та рівняння неперервності, від параметрів стану. Наприклад, при використанні закону фільтрації Дарсі рівняння стану можуть бути подані таким чином:

для нестисливих рідин і пористого середовища

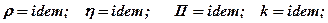
для баротропних рідин і пористого середовища

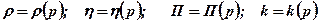
і т. п. Параметри пористого середовища (пласта) можуть залежати і від координат (наприклад, ).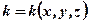

Граничні умови формулюються в залежності від суті задачі фільтрації. Їх має бути достатньо для одержання однозначного розв’язку задачі, тобто визначення постійних інтегрування. Початкові умови задають у задачах неусталеної фільтрації.

Об’ємна витрата нестисливої рідини при усталеній фільтрації за законом Дарсі в однорідному круговому пласті визначається формула Дюпюї:

,

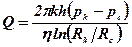де h – товщина пласта

R_c, R_k – відповідно радіуси свердловини та контуру пласта;

р_c, р_k – відповідно тиск у свердловині і тиск на контурі пласта.

Якщо 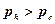, то свердловина буде проявляти з дебітом Q, а при 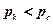– поглинати.

Величина 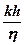називається гідропровідністю пласта.

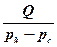
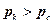Величина при називається коефіцієнтом продуктивності свердловини.

При ізотермічній фільтрації газу в аналогічних умовах формула Дюпюї набуває вигляду

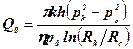(5.59)

де Q₀ – об’ємний дебіт газу при атмосферному тиску р₀ .

Усталена фільтрація нестисливої рідини за законом Форхгеймера в однорідному круговому пласті описується рівнянням

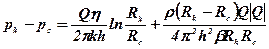. (5.60)

Для ізотермічної фільтрації газу в таких умовах справедлива формула

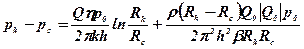. (5.61)

Відомі узагальнення формули Дюпюї на фільтрацію в неоднорідному за проникністю пласті. Наприклад, усталена фільтрація нестисливої рідини в пласт з дискретно змінною проникністю, яка моделює кірку, зону кольматації і власне пласт, описується рівнянням

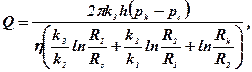(5.62)

де k₁, k₂, k₃ – проникності відповідно глинистої кірки, зони кольматації і пласта;

R_c, R_k – відповідно радіуси границь між глинистою кіркою і зоною кольматації, а також зоною кольматації і пластом.

У загальному випадку задача усталеної фільтрації нестисливої рідини за законом Дарсі в пористому середовищі з k=idem зводиться до інтегрування рівняння Лапласа

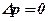(5.63)

з відповідними граничними умовами,

де 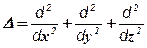– операція Лапласа.

Для лінійного закону фільтрації і баротропних рівнянь стану існує функція Христиановича:

,

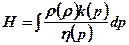яка задовольняє рівнянню .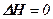

Це дає змогу використати принцип математичної аналогії: розв’язки задачі (3.11), які отримані для усталеної фільтрації нестисливої рідини, можна використовувати для розрахунків фільтрації баротропної рідини шляхом заміни тиску на функцію Хрисиановича.

При бурінні в результаті гідродинамічної взаємодії із свердловиною тиск у пласті змінюється. Наприклад, для однорідного кругового пласта і усталеної фільтрації, яка відповідає умовам формули Дюпюї, розподіл тиску у пласті визначається рівнянням

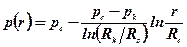. (5.64)

Для неоднорідного пласта, що відповідає умовам формули (5.62), розподіл тиску у пласті описується виразом

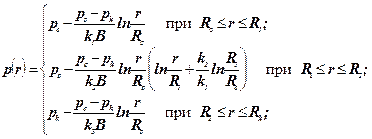(5.65)

де .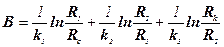

Поточне значення тиску в пласті називають динамічним пластовим тиском, який у деяких випадках визначає характер ускладнень при бурінні свердловини.

Диференціальне рівняння неусталеної фільтрації пружної рідини, яка відповідає закону Дарсі, в пружному пористому середовищі має вигляд

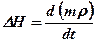. (5.66)

Для рівнянь стану

;

;

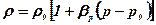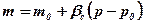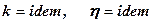
без урахування нелінійних складових правої частини формули (5.14) рівняння фільтрації набуває вигляду

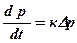, (5.67)

де 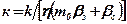–коефіцієнт п’єзопровідності пласта;

b_р, b_с – відповідно коефіцієнти об’ємного стиснення рідини і скелета гірської породи;

m₀, r₀ – відповідно пористість і густина породи при тиску р₀.

Коефіцієнт п’єзопровідності пласта характеризує швидкість перерозподілу тиску при неусталеній фільтрації пружної рідини в пружному пористому середовищі і змінюється в межах від 0,1 до 0,5 м²/с.

Рівняння (5.15) називається рівнянням п’єзопровідності, або основним диференціальним рівнянням пружного режиму. Для інтегрування рівняння (5.15) необхідно задати початкову та дві граничні умови.

Задача неусталеної радіальної фільтрації

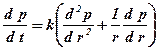
з початковими і граничними умовами

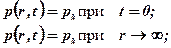
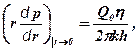
яка відповідає пуску свердловини в експлуатацію в момент часу t=0 з дебітом Q=idem, має розв’язок

,

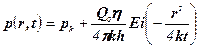де 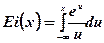– інтегральна показникова функція