Системы с параллельным соединением элементов

В параллельной структурной схеме соединения элементов надежности отказ всей системы произойдет лишь при отказе всех ее элементов. Т.е. система откажет тогда, когда откажут все ее элементы. Параллельное соединение элементов характерно для технических систем с дублированием или резервированием, т.е. для систем, в которых приняты меры по повышению надежности. Хотя нередки случаи, когда параллельное соединение (конструктивное и структурное) является естественным элементом конструкции. Например, сдвоенные колеса на полуоси заднего моста грузовика, двух и четырехмоторные самолеты и т.д.

Вероятность отказа системы с параллельным соединением элементов надежности равна произведению вероятностей отказов всех ее элементов:

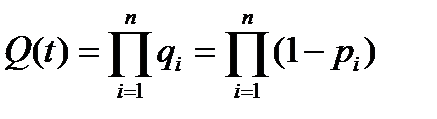. (47)

Следовательно: . (48)

Чем больше параллельных элементов, тем выше вероятность безотказной работы системы.

Если выделить самый надежный элемент системы k, то:

. (49)

Другими словами, вероятность безотказной работы системы из параллельных элементов надежности всегда выше вероятности безотказной работы самого надежного элемента. Значит, теоретически, из множества ненадежных элементов можно создать надежную систему при их параллельном соединении.

ПРИМЕР 12

Система состоит из равнонадежных параллельно соединенных элементов. Во сколько раз среднее время наработки до отказа такой системы больше среднего времени наработки до отказа элемента? Вычислить это увеличение для системы из двух элементов.

При экспоненциальном законе распределения вероятности безотказной работы системы из равнонадежных элементов можно записать:

, откуда среднее время безотказной работы системы равно:

. (50)

Т.е. среднее время наработки до отказа такой системы больше среднего времени наработки до отказа элемента в 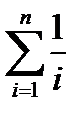раз.

При двух элементах этот коэффициент равен 1,5, при трех – 1,83.

Мажоритарная система представляет собой вариант системы с параллельным соединением элементов, в которой отказ происходит при потере работоспособности не всех ее элементов, а какой-то их части. Методы расчета надежности мажоритарных систем приведены в ПЗ 2.