Структурно-логический метод анализа системы

Структурно-логический анализ позволяет оценить основные показатели надежности объекта исходя из его конструктивных особенностей и взаимодействий составных частей, условий функционирования.

С точки зрения влияния на надежность системы в целом ее элементы подразделяют на четыре группы:

1. Элементы, отказ которых практически не влияет на работоспособность системы. Отказы этих элементов рассматриваются отдельно.

2. Элементы, работоспособность которых в течение рассматриваемой наработки практически не меняется, а вероятность их безотказной работы велика (близка к единице).

3. Элементы, ремонт или регулирование которых возможны в процессе работы или во время плановых остановок.

4. Элементы, отказ которых сам по себе или в сочетании с отказами других элементов приводит к отказу системы.

При анализе надежности системы в целом рационально рассматривать лишь элементы последней группы.

Большинство технических систем может быть представлено в виде совокупности элементов, соединенных последовательно или параллельно. Следует отметить, что параллельное или последовательное конструктивное исполнение элементов не всегда эквивалентно последовательному или параллельному соединению в схеме надежности.

В процессе структурно-логического анализа после проведения всех действий по выявлению возможных отказов, их причин и последствий, разделения системы на элементы с известными показателями надёжности, классификации этих элементов с точки зрения влияния на надёжность системы в целом, разрабатывается графическая модель безотказной работы, т.е. ее структурная схема надежности, по которой составляются расчетные зависимости для определения показателей надежности.

Методы минимального пути и минимального сечения

Минимальный путь (работоспособного состояния) – кратчайший путь функционирования; последовательный набор элементов в структурной схеме надежности, при котором система работоспособна, а отказ любого из этих элементов приводит к отказу системы.

Минимальное сечение (отказа) – минимальное аварийное сочетание; последовательный набор элементов в структурной схеме надежности, при котором система неработоспособна, а восстановление любого из этих элементов приводит систему в работоспособное состояние.

Эти методы эффективны при анализе мостиковых структурных схем надежности.

В мостиковых системах параллельные ветви элементов соединены между собой другими элементами. В простых случаях расчет надежности мостиковой системы может быть проведен методом прямого перебора, но с учетом положения элементов в схеме. Однако, в сложных системах формула работоспособного состояния (ФРС) сильно усложняется.

Если схема системы не сводится к одному из простых видов соединений, прибегают к логико-вероятностному методу ее анализа.

Рассмотрим пример простой мостиковой системы (рис. 12) и проанализируем ее надежность применяя логико-структурный метод.

ПРИМЕР № 14

Техническим аналогом мостиковой системы может, например, являться система с двумя параллельно включаемыми насосами (элементы 1 и 2), двумя регулирующими вентилями (элементы 4 и 5) и перепускным клапаном (элемент 3). Цель функционирования - бесперебойная подача топлива.

Логические формулы, отображающие работоспособное и неработоспособное состояния системы, имеют вид

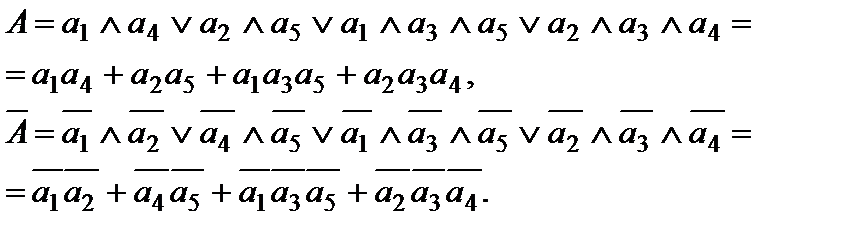
Логические формулы позволяют рассчитать показатели надежности системы, применяя теоремы сложения и умножения вероятностей.

С учетом сказанного, для системы по рис. 12 вероятность ее безотказной работы может быть вычислена по формуле

P=p₁p₄+p₂p₅+p₁p₃p₅+p₂p₃p₄–p₁p₂p₃p₄–p₁p₂p₃p₅–p₁p₂p₄p₅–p₁p₃p₄p₅–

–p₂p₃p₄p₅+2p₁p₂p₃p₄p₅.

Если все элементы системы равнонадежны, то P=2p²+2p³–5p⁴+2p⁵.

Логико-вероятностный метод довольно универсален, но в сложных случаях не всегда можно составить адекватную системе логическую функцию работоспособности. В теории надежности систем существуют методы рационализации логико-структурного метода. Мы их рассматривать не будем, поскольку это выходит за рамки нашего курса.