Топологические методы
Топологическими называют методы определения показателей надежности либо по графу состояний, либо по структурной схеме надежности. Этими методами, не прибегая к математическому моделированию технической системы, можно вычислить различные показатели надежности: вероятность безотказной работы при заданной наработке, среднюю наработку до отказа или на отказ, функцию и коэффициент готовности системы.
К достоинствам топологических методов относят: наглядность, простоту вычислений, допустимость приближенных оценок, возможность анализа надежности разнообразных систем (с восстановлением и без, с резервированием и без) при любой структурной схеме. Применение этих методов значительно усложняется в системах с переменными потоками отказов и восстановлений и в сложных системах, описываемых многосвязными графами состояний.
Топологический анализ надежности систем по графу состояний основан на том, что граф состояний полностью описывает все состояния системы и все переходы из одного состояния в другое (ЛР 5).
Ветви графа состояний представляют собой графическое изображение всех возможных переходов системы, причем, каждый элементарный переход (шаг) соответствует одному отказу или одному восстановлению элемента (рис. 15).
| ненагруженный резерв |
| последовательное |
| параллельное |
| λ2 |
| λ1 |
| λ1 |
| λ3 |
| λ2 |
| λ2 |
| λ1 |
| λ1 |
| λ2 |
| Рис.15. Графы состояний трех основных видов соединений. Цифры в кружках: верхние – шифр состояния элементов; нижние – номер состояния системы. Затемненные кружки – неработоспособное состояние системы. |
Основные правила построения графа состояний заключаются в следующем:
· Построение начинают с вершины, соответствующей работоспособному состоянию всех элементов.
· Все последующие вершины графа соответствуют состояниям последовательных отказов работоспособных элементов.
· Последующих состояний ровно столько, сколько работоспособных элементов может отказать в предыдущем состоянии.
· Новые состояния добавляются до тех пор, пока все состояния не станут неработоспособными.
· Неработоспособные состояния образуют конечные вершины графа.
· Состояния, отображающие одинаковые сочетания состояний элементов, образуют одну вершину графа (объединяются в одну вершину).
· При анализе сложных систем проводят их декомпозицию с целью построения графов подсистем.
· В системах с восстановлением элементов помимо прямых указываются и обратные переходы, отображающие восстановление элементов (с указанием интенсивности восстановления).
Рассмотрим построения графа состояний на примере невосстанавливаемой системы с ненагруженным резервом (рис. 16).
| Уровень 0 |
| Уровень 1 |
| Уровень 2 |
| Уровень 3 |
| Рис. 16. Граф состояний невосстанавливаемой системы с ненагруженным резервом. Эл. №5 не показан на 1-м уровне, т.к. он подключается только после выхода из строя эл. №4. |
На основе графов состояний составляются матрицы состояний и матрицы переходов, системы интегральных уравнений, а также определяются вероятности пребывания системы в данный момент в данном состоянии и, следовательно, определяются основные показатели надежности системы.
Функционирование любой восстанавливаемой системы полностью характеризуется матрицей состояний S размерностью m´n (m – число элементов (число строк), n – число состояний системы (число столбцов), равное числу вершин графа), столбы которой образуют векторы Ak. Для наглядности матрица состояний дополняется верхней строкой, содержащей соответствующие столбцам коды (или номера) состояний, и нижней строкой, в которой цифрой «1» обозначены работоспособные состояния системы, а «0» – неработоспособные.
В ЛР 5 рассмотрено построение матриц состояний и переходов на простой системе с дублированием и восстановлением элементов.
Если каждому состоянию системы (столбцу матрицы состояний) сопоставить функцию, аргументами которой служат компоненты соответствующего столбца плюс время, то эта функция есть плотность распределения вероятности пребывания системы в данном состоянии в данный момент времени
Еще одним графическим методом анализа надежности системы является метод построения дерева отказов. При построении дерева отказов реализуется дедуктивный метод – метод перехода от отказов элементов к отказу системы путем выявления причинно-следственных связей и построения соответствующей логической схемы. Эта схема, называемая деревом отказов, представляет собой ориентированный граф с ветвящейся структурой.
При построении дерева отказов используются обозначения, показанные на рис. 17.
Элемент логического сложения означает, что событие произойдет при любом одном происходящем событии на входе, элемент логического умножения – событие на выходе произойдет только при наличии всех событий на входе.
Для мостиковой системы по рис. 12 дерево отказов приведено на рис. 18.
В технике, как правило, встречаются системы, более сложные, чем рассмотренные выше. Первый шаг в анализе сложной системы – ее декомпозиция на подсистемы (блоки), которые поддаются анализу известными методами. Эту процедуру при необходимости можно повторить несколько раз. Затем составляется модель системы, состоящая из укрупнённых элементов, заменяющих собой уже исследованные подсистемы, для которых предварительно определены показатели надёжности. Такой метод анализа сложных систем называется методом свертки или методом эквивалентных преобразований.
| Рис. 17. Условные обозначения дерева отказов: 1, 2, 3 – результирующее, промежуточное и первичное события соответственно, 4 – элемент «ИЛИ» (логическое сложение), 5 – элемент «И» (логическое умножение) |
| входы входы |
При анализе надежности систем, выполняющих несколько функций, проводится раздельный анализ по каждой функции системы. Для каждой конкретной функции составляется своя структурная схема надежности.

|
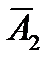
|
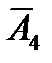
|
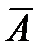
|
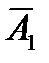
|
| G0 |
| G4 |
| G3 |
| G2 |
| G1 |
| Рис. 18. Дерево отказов системы по рис. 12 |
Дата добавления: 2015-03-19; просмотров: 1385;
