Системы с последовательным соединением элементов
В последовательной структурной схеме соединения элементов надежности отказ любого из элементов влечет за собой отказ всей системы. Другими словами, система работоспособна, когда все ее элементы работоспособны.
Системы с такой структурной схемой соединения элементов встречаются в технике чаще других, поэтому последовательное соединение называют основным соединением. В таких системах применима теорема умножения вероятностей: вероятность одновременного появления независимых событий равна произведению вероятностей этих событий.
Другими словами, вероятность безотказной работы в течение некоторой наработки t системы из n независимых друг от друга элементов P(t) равна произведению вероятностей безотказной работы элементов p(t):
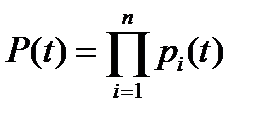 , (44)
, (44)
При значениях безотказной работы элементов, близких к единице, вероятность безотказной работы системы может быть оценена приближённо как:
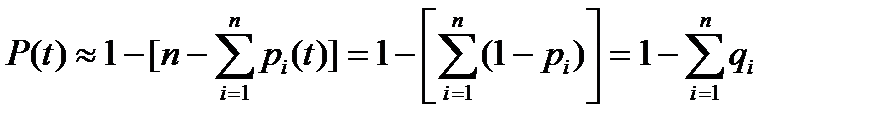 (45)
(45)
ПРИМЕР 9
Система состоит из n элементов высокой надежности. Вероятности безотказной работы элементов p близки к единице и практически одинаковы. Найти выражение для вероятности безотказной работы системы P и определить ее значение при n =2 и p =0,90; n =4 и p =0,99.
Для системы равнонадежных элементов справедливо равенство:
P=pn Тогда Р=0.92=0.81 и Р=0.994=0.96.
ПРИМЕР 10
Доказать, что надежность системы со схемой последовательного соединения независимых элементов всегда ниже надежности самого ненадежного элемента системы.
Очевидно, что вероятность безотказной работы подобных систем всегда ниже вероятности безотказной работы самого ненадежного элемента. Если выделить самый ненадежный элемент k, то можно записать:
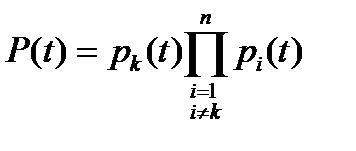 . Поскольку pi(t)<1, то и
. Поскольку pi(t)<1, то и 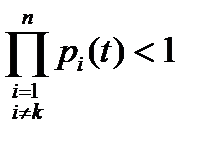 . Следовательно, P(t)<pk(t).
. Следовательно, P(t)<pk(t).
Из этого следует, что в случае неизбежного применения ненадежных элементов недопустимо составлять структурную схему с их последовательным соединением.
Для указанных условий справедливо(44).
ПРИМЕР 11
Доказать, что интенсивность отказов системы из последовательно соединенных элементов надежности в случае экспоненциального закона распределения вероятности безотказной работы каждого из этих элементов при постоянной интенсивности отказов элементов также постоянна и равна их сумме.
Для экспоненциального закона распределения вероятности безотказной работы каждого элемента системы и при постоянной интенсивности отказов справедливо равенство:
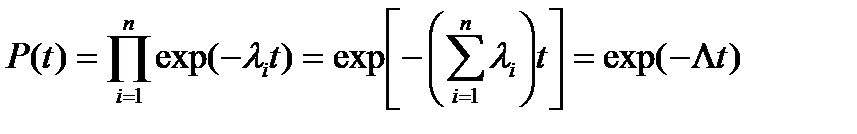 , (46)
, (46)
где 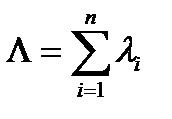 - интенсивность отказов системы в целом.
- интенсивность отказов системы в целом.
Таким образом, в рассмотренных условиях интенсивность отказов системы равна сумме интенсивностей отказов составляющих её элементов.
Средняя наработка системы до отказа будет при этом равна Т=1/Λ.
В системе с элементами равной надежности Λ=nλ, а Т=t/n. Т.е. средняя наработка системы в n раз меньше средней наработки каждого элемента. Из (46) следует:
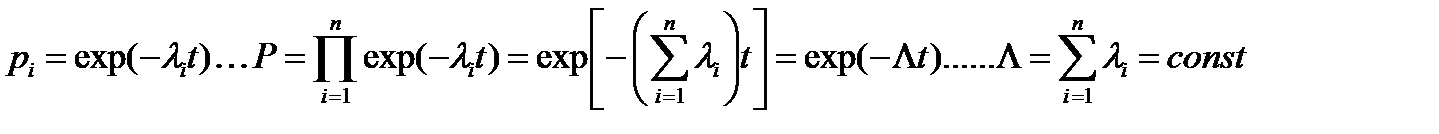
Дата добавления: 2015-03-19; просмотров: 1067;
