Методология моделирования надежности

Знание процессов и явлений, происходящих в элементах технического устройства, позволяет уменьшить число факторов, непредсказуемо влияющих на характеристики объекта. В то же время, количественные прогнозы надежности могут быть сделаны лишь при наличии модели отказов. Поскольку отказы имеют, как правило, вероятностный характер, то описывающие их модели будут стохастическими, или вероятностными. Разработка и широкое применение методов адекватного моделирования надежности позволяет существенно сократить, а иногда и полностью отказаться от дорогостоящих, трудоемких и длительных экспериментальных исследований при проектировании сложных технических систем. Некоторые режимы работы технических объектов вообще не могут быть исследованы экспериментально по причине их чрезвычайной опасности для здоровья или окружающей среды. Например, максимальные проектные или запроектные аварии на ядерных реакторах. Моделирование значительно расширяет возможности оптимизации устройства и не требует больших затрат ресурсов и времени. Однако, корректное формальное описание сложных, нелинейных и нестационарных процессов, к сожалению, не всегда возможно, или, по крайней мере, не всегда убедительно. Именно поэтому выработанный мировой практикой и широко используемый методологический подход заключается в следующем:

разрабатывается физико-математическая модель объекта;

разрабатывается расчетная схема и компьютерная программа;

компьютерная программа тестируется по экспериментальным данным;

корректируется расчетная модель объекта;

компьютерная программа верифицируется на известных, признанных как надежные и достоверные, экспериментальных данных;

если таких данных недостаточно, формируется, так называемая, стандартная задача, представляющая собой тщательно спланированный и хорошо оснащенный средствами контроля специальный эксперимент на крупномасштабной модели (принцип подобия при моделировании) технического объекта, которую принято называть «бенчмарк»;

сравнение и корректировка программ по данным, полученным в стандартной задаче на «бенчмарке»;

для легитимного применения программы в расчетах по конкретному проекту предусмотрена процедура ее валидации, т.е. утверждения в качестве средства адекватного описания характеристик объекта в обусловленных режимах работы, включая нештатные ситуации и аварийные состояния вплоть до максимальной проектной аварии.

Такой подход принят при обосновании надежности и безопасности потенциально опасных объектов, например, атомных станций. В менее ответственных случаях рациональность внедрения методов имитационного, т.е. вычислительного моделирования процессов функционирования объекта (принцип аналогии или частичного сходства при моделировании) ещё более очевидна.

Таким образом, исследования и оптимизация технических объектов с точки зрения повышения их надежности содержат теоретические, расчетные и экспериментальные работы. Причем эксперименты на стадиях разработки объекта носят характер определительных испытаний, а на стадии сдачи в эксплуатацию – контрольных. Контрольные испытания по-прежнему остаются единственным способом удостовериться в действительных показателях надёжности устройства, а определительные – важнейшим источником исходных данных для прогноза его надёжности.

В моделировании надежности первым и наиболее важным шагом является выбор физической модели объекта. Он может быть основан на статистическом анализе экспериментальных данных по надежности, полученных при испытаниях или при эксплуатации объекта.

Формализация физической модели надежности заключается в составлении математических выражений, описывающих: изменения определяющих надежность параметров от различных факторов и от времени, значения и изменения самих факторов, к каковым могут относиться механические, электрические, теплофизические и другие свойства материалов, а также внешние воздействия. Другими словами, в модели надежности ее показатель является функцией значений и изменчивости определяющих параметров надежности, которые, в свою очередь, функционально зависят от воздействующих факторов, в которые могут входить как характеристики свойств объекта, так и внешние факторы и время.

Например, вероятность отказа вследствие изменения i-того параметра qi(t) может быть выражена через скорость ее изменения во времени следующим образом:

,

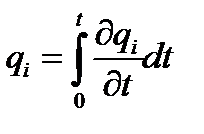а скорость изменения вероятности отказа может быть выражена через скорость изменения определяющего параметра Xi, который, в свою очередь, является функцией воздействующего фактора Zj:

.

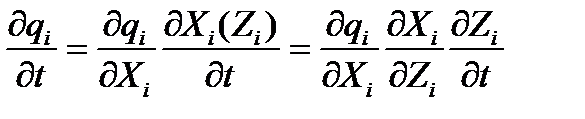Вероятность отказа от n учитываемых параметров равна:

.

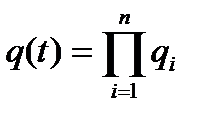Подчеркнём еще раз, что математическая модель надежности (в отличие от модели физических процессов) оперирует случайными величинами. Следовательно, законы надежности представляют собой выраженные в той или иной форме законы распределений случайных величин. Для оценки показателей надежности на основе вероятностной модели необходимо:

определить тип модели (вид распределения);

оценить параметры распределения;

определить показатели надежности.

В случаях, когда оцениваемые величины принимают счетное множество дискретных значений, применяются дискретные распределения. Для описания непрерывных случайных величин применяются непрерывные распределения. Иногда, при подгонке теоретических распределений к экспериментальным, прибегают к суммированию нескольких распределений. Это, как правило, распределения одного типа.

В заключение этого раздела подчеркнем, что анализ надежности объекта может проводиться на любом этапе жизненного цикла: при разработке, изготовлении, эксплуатации.