Плоской системы сходящихся сил (теорема Вариньона)
Момент равнодействующей плоской системы сходящихся сил относительно любой точки, лежащей в плоскости действия сил, равен алгебраической сумме моментов слагаемых сил относительно этой точки (рис. 2.11).
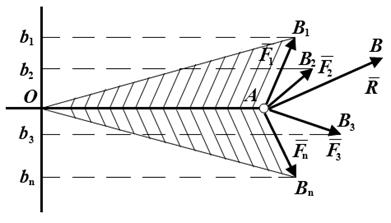
Рис. 2.11
Рассмотрим плоскую систему сил, сходящихся в точке А.
Выберем произвольную точку О и соединим ее с точкой А. Через точку О проведем ось Ох перпендикулярно ОА. Ось х направим так, чтобы проекция силы на эту ось и величина момента силы относительно точки О были одинакового знака. Спроецируем все силы на ось Ох: 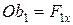 ,
, 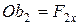 ,…,
,…,  .
.
Момент силы 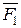 относительно точки О:
относительно точки О: 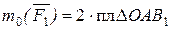 и т.д.
и т.д. 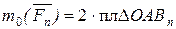 . Сложим сходящиеся силы. Равнодействующая сходящихся сил равна
. Сложим сходящиеся силы. Равнодействующая сходящихся сил равна 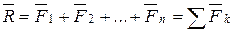 . Спроецируем векторное равенство на ось Ох:
. Спроецируем векторное равенство на ось Ох: 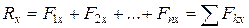 . Умножим левую и правую части полученного выражения на ОА, получим:
. Умножим левую и правую части полученного выражения на ОА, получим: 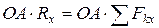 ,
, 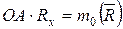 ,
, 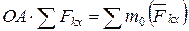 . Следовательно,
. Следовательно,  =
= 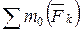 .
.
Теорема доказана.
Эта теорема позволяет определить момент силы относительно центра в том случае, если определение плеча силы вызывает затруднение.
Пример. Определить момент силы 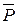 , приложенной к раме, относительно точки А (рис. 2.12). Разложим силу
, приложенной к раме, относительно точки А (рис. 2.12). Разложим силу 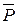 на составляющие
на составляющие 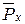 и
и 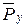 и определим их моменты относительно выбранной точки.
и определим их моменты относительно выбранной точки.
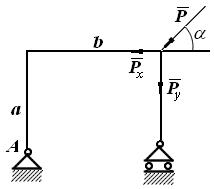
Рис. 2.12
Согласно теореме Вариньона:
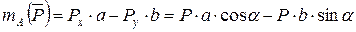 .
.
Дата добавления: 2015-03-17; просмотров: 1022;
