Теорема об эквивалентности пар

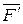Рассмотрим пару сил и , действующую на твёрдое тело (рис.2.8).

Проведём в плоскости действия пары через произвольные точки K и L две параллельные прямые до их пересечения с линиями действия сил 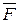и 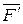. Перенесём силы и 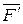в точки пересечения прямых А и В. Разложим силу на составляющие по направлениям AB и KB: 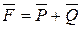, а силу 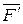- на составляющие по направлениям AB и AL: 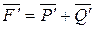Очевидно, что 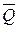и 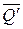можно отбросить, как уравновешенную систему сил. В результате пара ( , 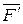) заменяется парой ( 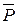, 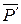) с плечом d₂.

Покажем, что пары ( , 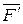) и ( 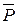, 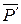) имеют одинаковые моменты:

m₁ = F·d₁, m₂ = Р·d₂;

m₁ = 2 · пл.∆АВВ´´;

m₂ = 2 · пл.∆АВВ´.

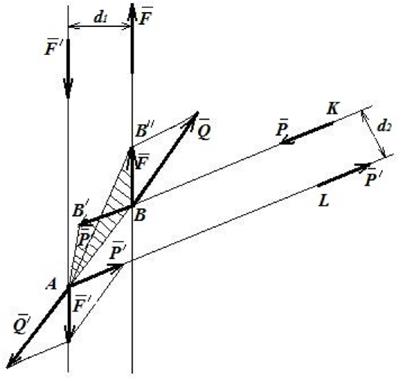
Рис. 2.8

Площади треугольников АВВ´´ и АВВ´ равны, так как у них общее основание АВ и одинаковая высота, т.к. АВ||В´В´´.

Следовательно: m₁ = F·d₁ = m₂ = Р·d₂.

Силы 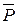и 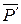можно перенести вдоль линии их действия и приложить к точкам K и L. По теореме об эквивалентности пар: пару сил, действующую на твёрдое тело, можно заменить другой парой, расположенной в той же плоскости и имеющей тот же алгебраический момент.

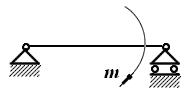
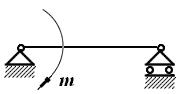
Из доказанной теоремы следует, что пару сил можно переносить в плоскости действия пары (рис. 2.9а и б) и у данной пары можно произвольно менять модуль силы и длину плеча, сохраняя неизменным её момент.

а	б

Рис. 2.9

На чертежах пару сил принято изображать изогнутым вектором с указанием величины момента.