Момент силы относительно центра
Момент силы  относительно центра О есть вектор
относительно центра О есть вектор 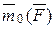 , приложенный в этом центре, который направлен перпендикулярно плоскости, проходящей через центр О и силу
, приложенный в этом центре, который направлен перпендикулярно плоскости, проходящей через центр О и силу  , в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки (рис. 2.3а).
, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки (рис. 2.3а).
Момент силы  относительно центра О равен векторному произведению радиуса-вектора, проведенного из центра О в точку А, где приложена сила, на саму силу:
относительно центра О равен векторному произведению радиуса-вектора, проведенного из центра О в точку А, где приложена сила, на саму силу:
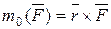 .
.
Момент силы  относительно центра О характеризуется:
относительно центра О характеризуется:
1) положением в пространстве плоскости ОАВ (плоскости поворота), проходящей через центр О и силу  ;
;
2) направлением поворота;
3) модулем момента силы.
Модуль момента силы определяется по правилу умножения векторов: модуль векторного произведения двух векторов равен произведению модулей этих векторов на синус угла между ними:
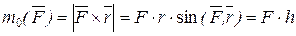 ,
,
т.к. 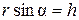 , где h – кратчайшее расстояние от точки О до линии действия силы
, где h – кратчайшее расстояние от точки О до линии действия силы  - называется плечом силы.
- называется плечом силы.
Алгебраическим моментом силы относительно точки называется скалярная величина, равная произведению модуля силы на плече силы относительно этой точки.
Плечом силы  относительно точки называется кратчайшее расстояние h от этой точки до линии действия силы.
относительно точки называется кратчайшее расстояние h от этой точки до линии действия силы.
Если сила стремится повернуть тело против хода часовой стрелки, то величина момента силы берётся со знаком «плюс», если по ходу часовой стрелки – знак «минус».
Свойства момента силы:
а) момент силы равен нулю, если сила равна нулю или когда плечо равно нулю, т.е. линия действия силы проходит через моментную точку,
б) величина момента силы относительно точки не изменяется при переносе силы вдоль линии её действия,
в) момент силы численно равен удвоенной площади треугольника, построенного на силе F и полюсе О (рис.2.3б).
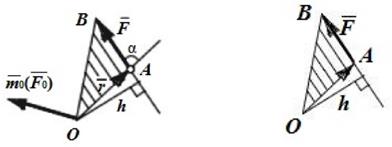
| а | б |
Рис.2.3
Пл. DOAB = ½ AB·h = ½ F·h. mo( 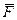 ) = Fh = 2·пл DOAB.
) = Fh = 2·пл DOAB.
Таким образом, алгебраический моменты силы  относительно точки О равен:
относительно точки О равен: 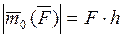 (Н∙м).
(Н∙м).
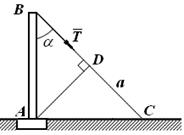
Рис. 2.4
Пример. Веревка ВС длиной а, привязанная к столбу под углом α, натягивается с силой, величина которой равна Т (рис. 2.4). Определить момент этой силы относительно точки А.
Решение.
Проведем перпендикуляр AD из точки А на линию действия силы 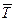 . Из треугольника АВD имеем:
. Из треугольника АВD имеем:  .
.
Так как сила  стремится вращать столб АВ вокруг точки А по ходу часовой стрелки, то момент силы
стремится вращать столб АВ вокруг точки А по ходу часовой стрелки, то момент силы  относительно точки А – отрицателен, т.е.
относительно точки А – отрицателен, т.е. 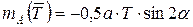 .
.
Дата добавления: 2015-03-17; просмотров: 1165;
