По исследованию условий равновесия системы сходящихся сил

Задачи данного типа могут решаться либо геометрическим (графическим) способом, либо аналитическим. При решении задач геометрическим (графическим) способом необходимо придерживаться следующего порядка:

1. Выделить тело (или точку), равновесие которого следует рассмотреть.

2. Изобразить все активные (заданные) силы, действующие на выделенное тело.

3. Освободить это тело от наложенных на него связей, заменив их действие реакциями связей.

4. Построить замкнутый силовой многоугольник (или треугольник – если действуют три силы). При этом следует сначала сложить все заданные, а затем достроить неизвестные силы.

5. Решить силовой многоугольник (по известным элементам определить неизвестные) или, если силовой многоугольник построен в масштабе, определить искомые силы по масштабу.

При решении задач аналитическим способом рекомендуется придерживаться следующего порядка:

1. Выделить точку, равновесие которой надо рассмотреть.

2. Изобразить активные (заданные) силы.

3. Освободить точку от связей, приложив соответствующие реакции. При этом необходимо убедиться, что данная задача является статически определимой – число неизвестных величин должно быть не более двух или трех (в случаях плоской и пространственной систем сходящихся сил соответственно).

4. Направить оси координат.

5. Составить уравнения равновесия системы сходящихся сил, из которых можно найти неизвестные величины.

Пример.Стержни АС и ВС соединены между собой и с вертикальной стеной посредством шарниров (рис. 1.31). На шарнирный болт С действует вертикальная сила Р = 1000 Н.

Определить реакции этих стержней на шарнирный болт С, если углы, составляемые стержнями со стеной, равны: α = 30° и β = 60°.

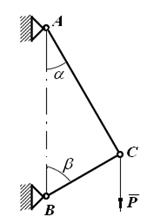
Рис. 1.31

Задачу можно решить либо аналитически, либо графически.

I. Геометрический способ. Очевидно, что объектом исследования в данной задаче является болт C, т.к. именно к нему приложены заданная сила 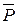и стержни AC и BC, реакции которых нужно определить. Отбросим связи, заменив их действие реакциями.

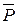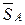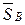Построим замкнутый треугольник abc (рис. 1.32) для сил , и (т.к. болт C находится в равновесии), начав построение с известной силы 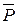, которую изобразим вектором 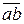, тогда вектор 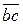определит силу 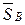, а вектор 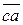- силу 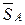. При этом следует учесть, что известны только направления реакций связей.

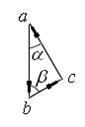
Рис. 1.32

Измерив отрезк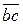и и 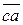выбранной единицей масштаба, найдем величины неизвестных сил 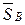и 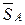и задача будет графически решена.

Величины неизвестных сил 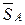и 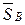можно найти тригонометрически, решив силовой треугольник abc, т.е. в этом треугольнике известны сторона ab и два угла α и β.

Итак, построим в масштабе вектор 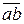(который, как и 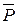, направлен вертикально вниз) из точки a под углом α прведем одну линию, из точки b проведем вторую линию под углом β до пересечения их в точке с, треугольники ΔАВС и Δabc подобны.

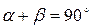- по условию задачи, следовательно, Δabc – прямоугольный. Из этого треугольника находим:

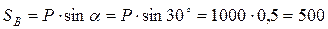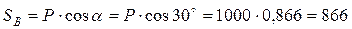Н

Н.

II. Аналитический способ. Выполним пункты 1-3 аналогично, как и при решении задачи графическим способом. Поэтому продолжим решение данной задачи с пункта 4 – выберем систему координат. Так как угол между неизвестными силам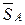и и 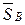равен 90°, то удобнее всего направить по линиям действия этих сил оси координат.

Направим Ох по линии действия 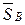, а ось Оу – по линии действия 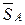(рис. 1.33).

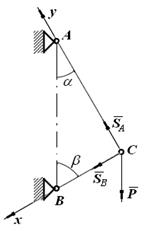
Рис. 1.33

Для данной плоской системы сходящихся сил составим 2 уравнения равновесия:

; ;

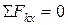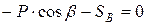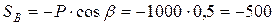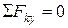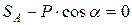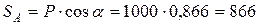Н.

; ;

Н.

При аналитическом способе заранее неизвестно, в какую сторону направить реакции стрежней вдоль прямых АС и ВС. Если в результате решения получим положительные значения, то реакции были направлены верно, если получим отрицательные, то выбранное направление реакции изменим на противоположное.