Теорема о параллельном переносе силы (метод Пуансо)

Пусть на тело действует сила , приложенная в точке А (рис.2.18).

Действие этой силы не изменится (согласно второй аксиоме статики), если в произвольной точке В тела приложить две уравновешенные силы 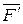и 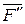, такие, что 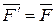, , 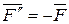причем обе силы параллельны . Полученная система трех сил и представляет собой силу 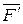равную , но приложенную в точке В, и пару ( , 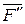), момент которой равен m = m_B ( ).

Следовательно, силу, приложенную к абсолютно твёрдому телу, можно не изменяя оказываемого ею действия, переносить параллельно ей самой из данной точки в любую другую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда эта сила переносится. Тогда 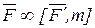, где 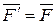, m=m_B( ).

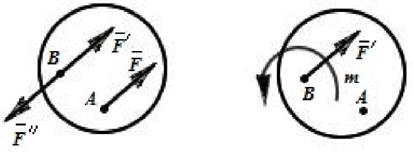
Рис. 2.18

Пример. Чтобы удержать в равновесии однородный брус АВ длиной 2а и весом 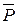, надо приложить в его середине С направленную вверх силу 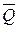, по модулю равную 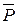(рис. 2.19).

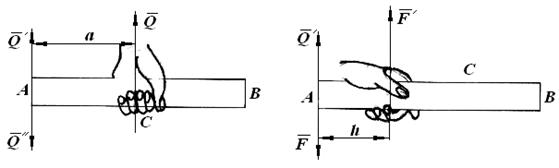
Рис. 2.19

Согласно доказанной теореме силу 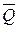можно заменить силой 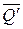, приложенной к концу А бруса и парой с моментом, модуль которого 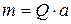. Если плечо этой пары уменьшить до величины h, то образующие ее силы и 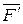надо увеличить так, чтобы 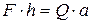. Следовательно, чтобы удержать брус за конец А, надо, кроме силы 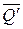, приложить еще пару , 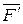. Этот результат, вытекающий из теоремы «ощущает» рука человека, удерживающего брус за середину или за конец.