Оптико-механическая аналогия Гамильтона. 5 страница

и как следствие:

Волновую функцию в этом случае представляем в виде:

или

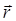Амплитуда в этих выражениях слабо зависит от , то есть намного меньше, чем . Пример этому – сферическая волна при . Поэтому в дальнейших выкладках считаем константой. Проводим вычисления только для одномерной задачи:

Подставим уравнение волны в соответствующее волновое уравнение:

Вычисления дают:

Вторая производная в полученном выражении считается намного меньшей квадрата первой (локально почти плоские волны). Поэтому, соответственно:

По тем же причинам , так что – преобладающий член по сравнению с и таким образом:

Соответственно, волновое уравнение:

переходит в уравнение для фазы:

Но градиент фазы есть локальный волновой вектор:

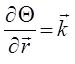
С его длиной можно отождествить частоту:

и соответственно:

Сравнивая полученные выше выражения:

и

видим, что с точностью до знака, полностью совпадает с частотой . Пример плоской волны , позволяет уточнить эту связь:

Итак, лучи характеризуются функцией координат и времени – фазой , удовлетворяющей соотношениям:

где – касательный вектор луча. В то же время механические траектории также характеризуются функцией координат и времени – действием , причём как было выяснено уже ранее:

Эта поразительная аналогия терминов механики частиц и оптики лучей:

имеет глубокое физическое содержание. Действительно, из аналогии:

следует, что вариационному принципу механики должен отвечать свой вариационный принцип в геометрической оптике. Вид последнего легко показать, пользуясь соответствием:

Частота как аналог энергии 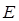на всём пути (луче) должна оставаться неизменной. Физически это обеспечивается стационарностью оптической среды – неизменностью во времени функции . Оптико-механическая аналогия наводит на мысль, а не является ли сама классическая механика (как аналог геометрической оптики) предельным случаем некоторой более общей теории.

В самом деле, аналогию:

можно углубить, введя коэффициент перехода между величинами справа и слева. Обозначив этот коэффициент 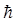, будем иметь соответственно:

то есть величина 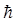является универсальным коэффициентом перехода от волновых понятий к механическим. Очевидно, что 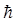имеет размерность действия, где – безразмерная величина. Видно, что требование для выполнения геометрической оптики означает, условием справедливости классической механики можно считать предел, при котором:

Рассуждения, приведшие к уравнениям:

а также пределу отношения:

стали возможны лишь с обнаружением экспериментальных фактов, не укладывающихся в рамки привычного классического описания. Многочисленные исследования привели к необходимости создания более общей теории, которую поначалу называли волновой механикой. Однако наиболее существенной стороной новой теории было квантование – существование для многих физических величин лишь дискретного ряда допустимых значений. Поэтому термин «волновая механика» со временем уступил место более современному – «квантовая механика».