Оптико-механическая аналогия Гамильтона. 3 страница

или после взятия производной функции, с последующим возведением в квадрат результатов дифференцирования, приходим к соответствующим промежуточным результатам для каждой из пространственных координат:
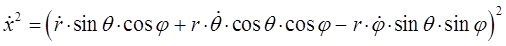
откуда:
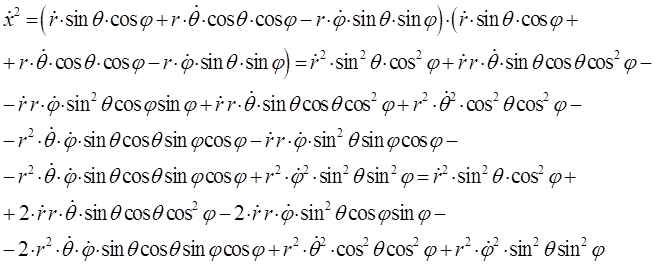
и аналогично:
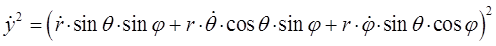
откуда:
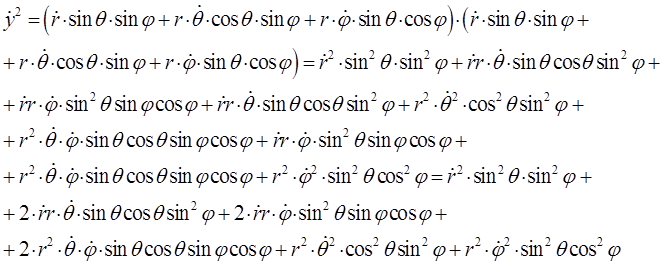
а также:
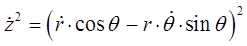
откуда:
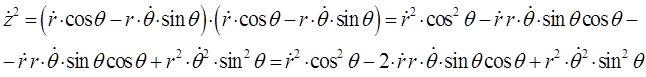
Таким образом, имеем:
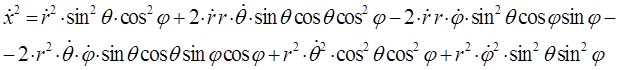
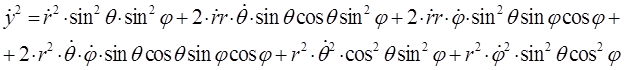
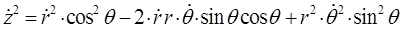
Складывая между собой полученные выражения для каждой из компонент, будем иметь соответственно:
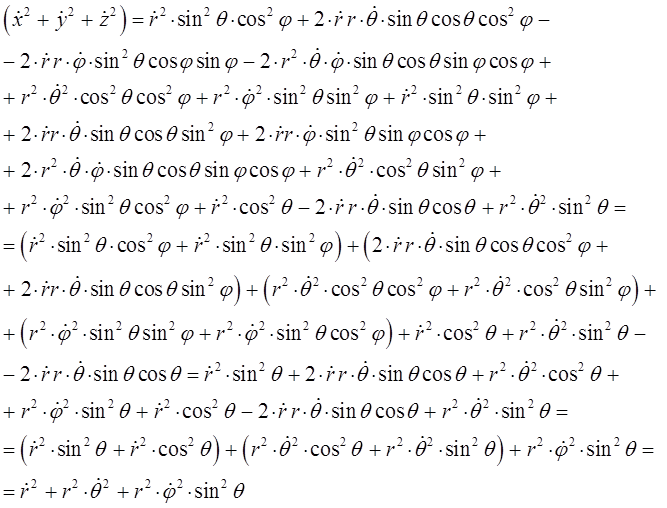
или в окончательном виде:
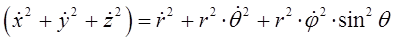
Учитывая, что:
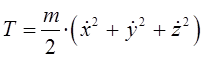
имеем:

Выразим теперь кинетическую энергию через импульсы в сферической системе координат. С учётом уравнений Гамильтона:
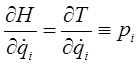
выражение для кинетической энергии в сферической системе координат, очевидно, может быть переписано в виде:
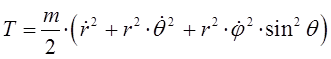
Дифференцирование выражения для кинетической энергии по каждой из обобщённых координат, даёт выражения вида:
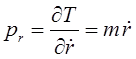
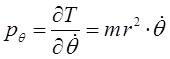
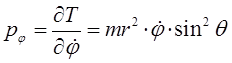
поскольку:
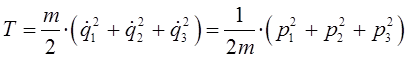
а также с учётом того, что:
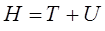
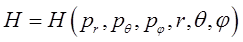
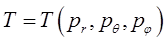

будем для гамильтониана соответственно иметь выражение вида:
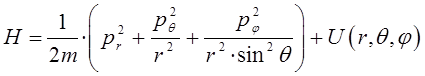
где
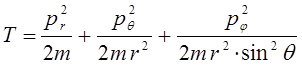
Таким образом, в ходе проделанных выкладок, приходим к выражениям для гамильтониана соответственно в полярной:
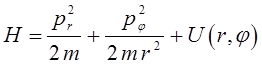
и сферической системах координат:
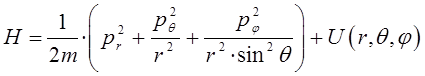
где
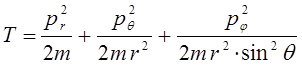
Рассмотрим плоское движение частицы по орбите в плоскости  . Учитывая плоский характер орбиты, направим ось
. Учитывая плоский характер орбиты, направим ось  вдоль постоянного вектора
вдоль постоянного вектора 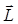 :
:
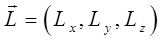
При таком выборе декартовой системы координат, две компоненты вектора момента импульса частицы 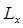 и
и 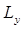 очевидно будут равняться нулю. Тогда, вектор момента импульса (углового момента) можно записать как:
очевидно будут равняться нулю. Тогда, вектор момента импульса (углового момента) можно записать как:
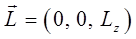
и движение совершается в плоскости, перпендикулярной оси 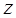 . Из-за сохранения сектора
. Из-за сохранения сектора 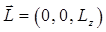 , значение угла
, значение угла  сохраняется:
сохраняется:
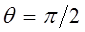

следовательно:
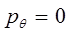
и гамильтониан:
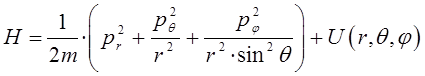
после подстановки соответствующих граничных условий, очевидно, может быть сведен к виду:
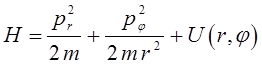
Таким образом, при рассмотрении плоского движения частицы мы в равной мере можем пользоваться как полярной, так и сферической системами координат.
Покажем теперь, что импульс 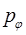 на самом деле совпадает с
на самом деле совпадает с 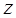 - компонентой момента импульса
- компонентой момента импульса 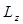 . Для этого раскроем
. Для этого раскроем 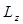 как векторное произведение:
как векторное произведение:
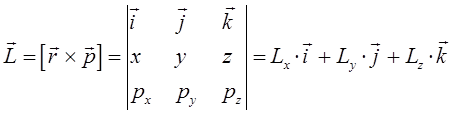
Заметим, что вычисление скобок Пуассона приводит к соотношениям вида:
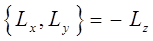
остальные же получают на основании правила циклической перестановки индексов, на основании которого можно легко получить аналитическое выражение для соответствующих проекций момента импульса:
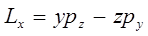
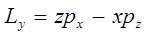
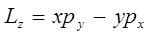
Действительно, поскольку:
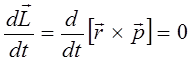
и как следствие:
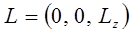
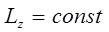
то можно ограничиться только одной из проекций углового момента:

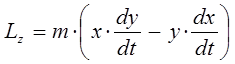
поскольку по определению:
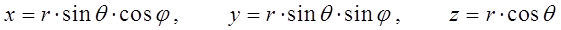
тогда после подстановки данных значений переменных в выражение проекции момента импульса на ось 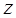 , будем иметь соответственно:
, будем иметь соответственно:
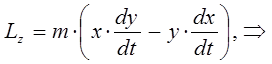
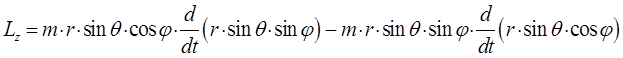
раскрывая в полученном выражении скобки и учитывая, что:
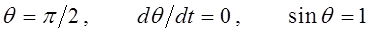
будем иметь соответственно:
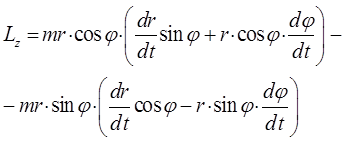
откуда следует, что:
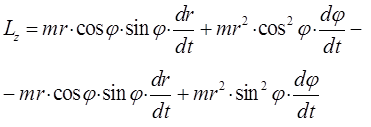
преобразуя полученное выражение к виду:
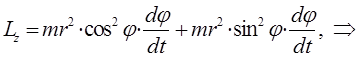
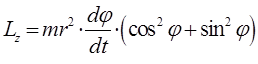
будем иметь соответственно:
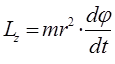
и таким образом:

Поэтому выражение для гамильтониана:

с учётом приведенных выше рассуждений можно будет представить далее к виду:

Поскольку для вектора:
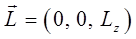
оказывается справедливым:
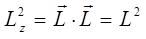
имеем соответственно:

Именно такого рода гамильтонианом описывают движение электрона в атоме водорода. Найдём условия движения частицы по кругу. Так, например, если частица совершает устойчивое круговое движение в центральном силовом поле (поле постоянного потенциала), то очевидно её радиус будет являться постоянным:
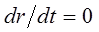
отсюда следует, что первый член в выражении для энергии будет равен нулю:
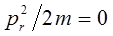
В связи с этим удобно ввести так называемый эффективный потенциал:
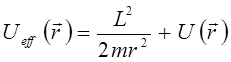
Очевидно, частица будет совершать круговое движение 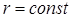 , при условии, что производная по радиусу от эффективного потенциала
, при условии, что производная по радиусу от эффективного потенциала  равна нулю:
равна нулю:
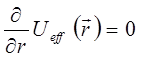
Учитывая выражение для потенциальной энергии:
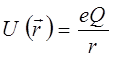
имеем:
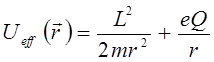
Выясним, как ведут себя разноименные взаимодействующие между собой заряды; т.е. задача будет сводиться к выяснению характера их взаимодействия. Для этого вычислим производную от  по
по 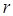 и приравняем её нулю. В результате получим выражение вида:
и приравняем её нулю. В результате получим выражение вида:
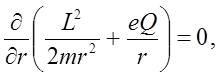
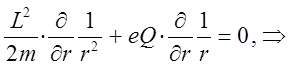

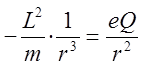
Поскольку левая часть в полученном выражении отрицательна, необходимо, чтобы произведение зарядов имело отрицательный знак:
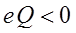
что в свою очередь будет соответствовать притяжению разноимённо заряженных частиц. Необходимо также отметить, что выражение:
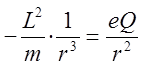
является условием равновесия двух сил: центробежного отталкивания (левая часть) и кулоновского притяжения (правая часть). Действительно, поскольку по определению:
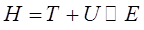
тогда для всех допустимых значений 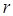 , будем иметь соответственно:
, будем иметь соответственно:
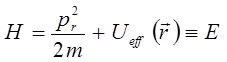
из не отрицательности 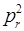 следует требование:
следует требование:

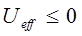
Данные неравенства задают допустимую область изменения 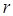 . Так, неравенства:
. Так, неравенства:
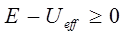
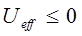
показывают, что при 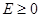 область движения становится не ограниченной – движение инфинитное. В этом случае эффективная сила
область движения становится не ограниченной – движение инфинитное. В этом случае эффективная сила 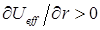 - направлена от центра, и частица уходит в бесконечность. Иными словами, инфинитному движению соответствует несвязанное состояние. При
- направлена от центра, и частица уходит в бесконечность. Иными словами, инфинитному движению соответствует несвязанное состояние. При 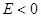 , движение совершается в ограниченной области пространства – финитное движение. В данном случае частица находится вблизи силового центра, а эффективная сила направлена к силовому центру, связанному с частицей
, движение совершается в ограниченной области пространства – финитное движение. В данном случае частица находится вблизи силового центра, а эффективная сила направлена к силовому центру, связанному с частицей 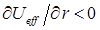 .
.
3.1.4.2. Многочастичные колебательные системы.
Исследуем теперь колебательные движения системы с  степенями свободы относительно некоторого устойчивого её равновесного положения. Это значит, что существуют значения
степенями свободы относительно некоторого устойчивого её равновесного положения. Это значит, что существуют значения 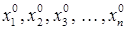 обобщённых координат
обобщённых координат 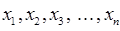 , когда силы отсутствуют:
, когда силы отсутствуют:
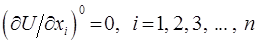
и система покоится. Выведем систему из равновесия, придав каждому равновесному значению 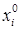 некоторую малую добавку
некоторую малую добавку 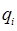 :
:

Разложим потенциальную энергию в ряд Тейлора:
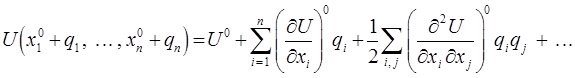
однако в силу равенства:
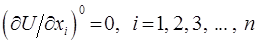
линейные по 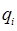 члены исчезают и при
члены исчезают и при 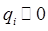 разложение:
разложение:
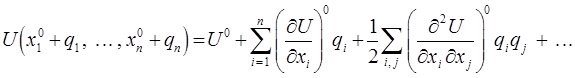
сводится к уравнению:
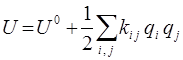
здесь:
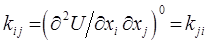
есть силовая постоянная, характеризующая упругость (сопротивление) системы при одновременном растяжении 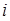 -той и
-той и 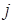 -той обобщённых координат. В ряде литературных источников данную константу называют ещё силовой постоянной. Необходимо отметить, что уравнения движения Ньютона в форме:
-той обобщённых координат. В ряде литературных источников данную константу называют ещё силовой постоянной. Необходимо отметить, что уравнения движения Ньютона в форме:
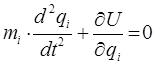
требуют в общем случае вычисления силы 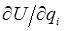 . Для этого более подробно запишем полученное нами уже ранее выражение. Так, имеем соответственно:
. Для этого более подробно запишем полученное нами уже ранее выражение. Так, имеем соответственно:
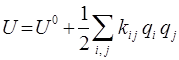
и соответственно:
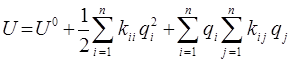
где учтено, что 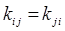 . Откуда становится очевидным, что уравнение:
. Откуда становится очевидным, что уравнение:
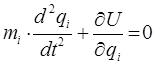
переходит в линейную однородную систему дифференциальных уравнений:
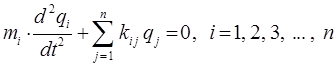
избавимся теперь от масс  переходом к «масс-взвешенным» координатам:
переходом к «масс-взвешенным» координатам:

а именно:
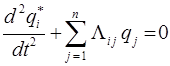
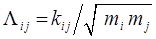
Решение данной системы, обобщающей уравнение:
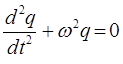
имеет гармонический вид:
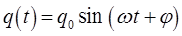
или если колебательный процесс в многочастичной системе имеет косинусоидальную зависимость, тогда:
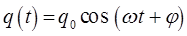
для каждой обобщённой координаты:
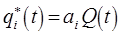

или
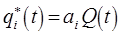
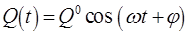
Числа 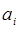 определяют вклад
определяют вклад 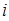 -той обобщённой координаты
-той обобщённой координаты 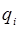 в коллективное колебание всей системы частиц, совершаемое с единой частотой
в коллективное колебание всей системы частиц, совершаемое с единой частотой  . Величины
. Величины 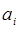 удобно нормировать как компоненты единичного вектора условием:
удобно нормировать как компоненты единичного вектора условием:

Тогда для данного колебания с частотой  величина
величина 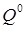 – максимально возможное смещение частицы. Рассмотренное согласованное гармоническое движение всех частиц называют собственным, или нормальным, колебанием системы. Числа
– максимально возможное смещение частицы. Рассмотренное согласованное гармоническое движение всех частиц называют собственным, или нормальным, колебанием системы. Числа 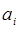 определяют так называемую форму нормального колебания. Нахождение частот и форм разрешённых нормальных колебаний сводится к решению алгебраической задачи. Подставив выражение условия нормировки в систему уравнений вида:
определяют так называемую форму нормального колебания. Нахождение частот и форм разрешённых нормальных колебаний сводится к решению алгебраической задачи. Подставив выражение условия нормировки в систему уравнений вида:
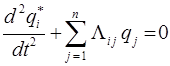
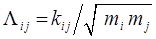
будем иметь соответственно:

Сократив уравнение:
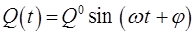
или
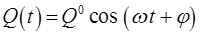
на ненулевую функцию 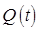 , получим систему линейных однородных уравнений для
, получим систему линейных однородных уравнений для 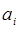 , то есть имеем соответственно:
, то есть имеем соответственно:

или в развёрнутом виде:
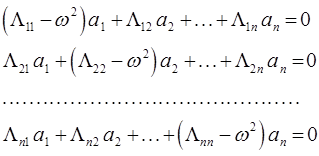
По теореме Кронекера – Капелли данная однородная система имеет нетривиальное решение только при нулевом значении детерминанта (определителя) системы:
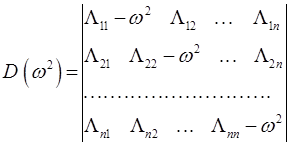
Если раскрыть определитель  , то по отношению к
, то по отношению к  он окажется к многочленом
он окажется к многочленом  -й степени уже за счёт произведения диагональных элементов:
-й степени уже за счёт произведения диагональных элементов:
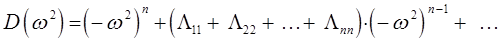
Полученный многочлен называют вековым многочленом, а систему уравнений вида:
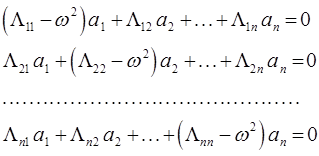
называют системой вековой, где уравнениями типа. Как известно, многочлен  -й степени имеет ровно
-й степени имеет ровно  комплексных корней, т.е.
комплексных корней, т.е.

Действительность всех корней 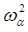 гарантируется симметричностью матрицы:
гарантируется симметричностью матрицы:

Однако положительность 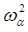 , а, следовательно, и возможность получения действительных частот
, а, следовательно, и возможность получения действительных частот 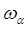 является следствие постулированной устойчивости механической системы. Теперь уточним общее решение рассмотренной выше системы вековых уравнений:
является следствие постулированной устойчивости механической системы. Теперь уточним общее решение рассмотренной выше системы вековых уравнений:
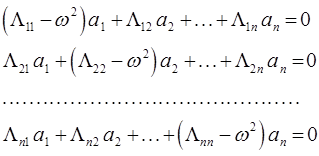
Зная  -ю частоту
-ю частоту 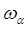 , находим из однородной системы вековых уравнений
, находим из однородной системы вековых уравнений  -й набор неизвестных величин
-й набор неизвестных величин 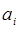 , нормированных условием вида:
, нормированных условием вида:

Более точно полученный набор величин следует обозначать через 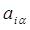 , явно указывая дополнительным индексом
, явно указывая дополнительным индексом  , для какой частоты
, для какой частоты 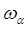 он получен. Тогда в терминах введенных нами выше обозначений, общие решения для
он получен. Тогда в терминах введенных нами выше обозначений, общие решения для  -й частоты будут иметь вид:
-й частоты будут иметь вид:
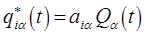
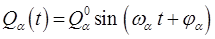
или
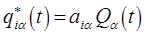
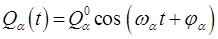
где 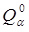 и
и 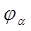 – амплитуда, и фаза
– амплитуда, и фаза  -го нормального колебания. Значениями
-го нормального колебания. Значениями 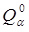 и
и 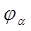 можно распорядиться так, чтобы учесть любые начальные условия. Общее решение представляет собой комбинацию соответствующих частных решений:
можно распорядиться так, чтобы учесть любые начальные условия. Общее решение представляет собой комбинацию соответствующих частных решений:
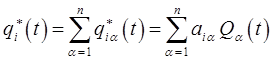
Таким образом, 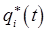 оказывается линейной комбинацией «гармонических» координат
оказывается линейной комбинацией «гармонических» координат  :
:
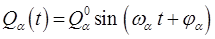
или
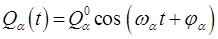
Каждая из гармонических координат  совершает независимое колебание со своей частотой
совершает независимое колебание со своей частотой 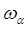 и называется нормальной. В этих терминах выражение:
и называется нормальной. В этих терминах выражение:
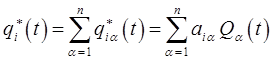
есть разложение произвольного колебания системы на нормальные колебания. Рассмотрим простейший пример колебаний системы с двумя степенями свободы:
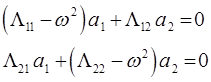
Вековое уравнение этой системы:
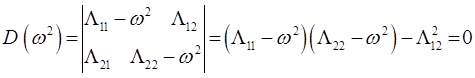
Для симметричного случая, то есть когда 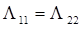 , уравнение:
, уравнение:
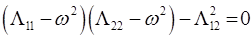
имеет простые решения вида:
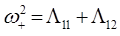
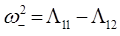
Подставляя значения 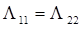 и
и 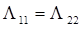 в систему:
в систему:
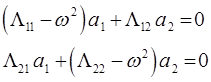
находим коэффициенты формы колебаний 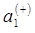 ,
, 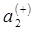 для
для 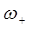 и
и 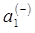 ,
, 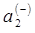 для
для 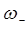 и таким образом имеем соответственно:
и таким образом имеем соответственно:

где учтено требование нормировки:
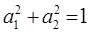
В рамках рассматриваемой задачи частота 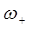 , как видно отсюда, будет отвечать симметричному колебанию, а
, как видно отсюда, будет отвечать симметричному колебанию, а 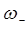 – антисимметричному. Это же видно и из разложения:
– антисимметричному. Это же видно и из разложения:
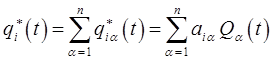
по нормальным координатам 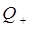 и
и 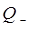 данной задачи, то есть имеем:
данной задачи, то есть имеем:

Колебательные системы обнаруживают качественно новые черты, когда число частиц  , связанных силами упругости, становится настолько большим, что в совокупности все частицы составляют уже непрерывную среду. Например, пусть дана цепочка
, связанных силами упругости, становится настолько большим, что в совокупности все частицы составляют уже непрерывную среду. Например, пусть дана цепочка  одинаковых части, очень плотно заполняющих интервал
одинаковых части, очень плотно заполняющих интервал 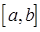 оси
оси 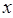 . В первом приближении упругая сила пропорциональна изменению расстояния между частицами. Поэтому для U принимается выражение, аналогичное тому, что было получено нами для случая одночастичных колебательных систем. Так, разлагая потенциал U в ряд Тейлора, имеем соответственно:
. В первом приближении упругая сила пропорциональна изменению расстояния между частицами. Поэтому для U принимается выражение, аналогичное тому, что было получено нами для случая одночастичных колебательных систем. Так, разлагая потенциал U в ряд Тейлора, имеем соответственно:
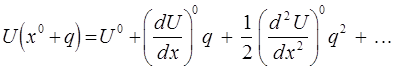
Величину  в данном выражении называют также равновесным расстоянием. При малых отклонениях от положения равновесия
в данном выражении называют также равновесным расстоянием. При малых отклонениях от положения равновесия 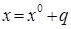 , где
, где 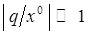 . Верхний индекс
. Верхний индекс  показывает, что величина вычислена в точке равновесия. Поскольку в случае одночастичных колебательных систем оказывается справедливым условие:
показывает, что величина вычислена в точке равновесия. Поскольку в случае одночастичных колебательных систем оказывается справедливым условие:
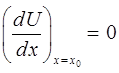
линейный по 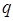 член в выражении:
член в выражении:
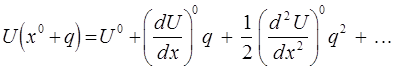
исчезает и с большей степенью точности:
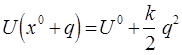
Дата добавления: 2015-03-14; просмотров: 844;
