Электромагнитная теория Максвелла. Волновое уравнение. Уравнение волны. Электрическая и магнитная компоненты электромагнитного излучения.

Примерно к 1860 г. благодаря работам Неймана, Вебера, Гельмгольца и Феличи электродинамика считалась уже наукой окончательно систематизированной, с чётко определёнными границами. Основные исследования теперь уже, казалось, должны были идти по пути нахождения и вывода всех следствий из установленных принципов и их практического применения. Однако перспективу такой спокойной работы нарушил молодой шотландский физик Джемс Кларк Максвелл (1831—1879), указав на гораздо более широкую область применений электродинамики. С полным основанием Дюэм писал: «Никакая логическая необходимость не толкала Максвелла придумывать новую электродинамику; он руководствовался лишь некоторыми аналогиями и желанием завершить работу Фарадея в таком же духе, как труды Кулона и Пуассона были завершены электродинамикой Ампера, а также, возможно, интуитивным ощущением электромагнитной природы света». Быть может, основным побуждением, которое заставило Максвелла заняться работой, вовсе не требовавшейся наукой тех лет, было восхищение новыми идеями Фарадея, столь оригинальными, что учёные того времени не способны были воспринять их и усвоить. Поколению физиков-теоретиков, воспитанных на понятиях и математическом изяществе работ Лапласа, Пуассона и Ампера, мысли Фарадея казались слишком расплывчатыми, а физикам-экспериментаторам - слишком мудрёными и абстрактными. Фарадей, который по своему образованию не был математиком, начав свою карьеру разносчиком в книжной лавке, а затем, поступив в лабораторию Дэви на положение ассистента, чувствовал настоятельную необходимость в разработке некоего теоретического метода, столь же действенного, как и математические уравнения. В предисловии к своему знаменитому «Трактату»

Максвелл писал: «Приступив к изучению труда Фарадея, я установил, что его метод понимания явлений был также математическим, хотя и не представленным в форме обычных математических символов, Я также нашёл, что этот метод можно выразить в обычной математической форме и, таким образом, сравнить с методами профессиональных математиков. Так, например, Фарадей видел силовые линии, пронизывающие всё пространство, там, где математики видели центры сил, притягивающих на расстоянии; Фарадей видел среду там, где они не видели ничего, кроме расстояния; Фарадей предполагал источник и причину явлений в реальных действиях, протекающих в среде, они же были удовлетворены тем, что нашли их в силе действия на расстоянии, приписанной электрическим флюидам. Когда я переводил то, что я считал идеями Фарадея, в математическую форму, я нашел, что в большинстве случаев результаты обоих методов совпадали, так что ими объяснялись одни и те же явления и выводились одни и те же законы действия, но что методы Фарадея походили на те, при которых мы начинаем с целого и приходим к частному путём анализа, в то время как обычные математические методы основаны на принципе движения от частностей и построения целого путем синтеза. Я также нашел, что многие из открытых математиками плодотворных методов исследования могли быть значительно лучше выражены с помощью идей, вытекающих из работ Фарадея, чем в их оригинальной форме». Что же касается математического метода Фарадея, Максвелл в другом месте замечает, что математики, которые считали метод Фарадея лишённым научной точности, сами не придумали ничего лучшего, как использование гипотез о взаимодействии вещей, не обладающих физической реальностью, как, например, элементов тока, «которые возникают из ничего, проходят участок провода и затем снова превращаются в ничто». Чтобы придать идеям Фарадея математическую форму, Максвелл начал с того, что создал электродинамику диэлектриков. Теория Максвелла непосредственно связана с теорией Моссотти. В то время как Фарадей в своей теории диэлектрической поляризации намеренно оставил открытым вопрос о природе электричества, Моссотти, сторонник идей Франклина, представляет себе электричество как единый флюид, который он называет эфиром и который, по его мнению, присутствует с определенной степенью плотности во всех молекулах. Когда молекула находится под действием силы индукции, эфир концентрируется на одном конце молекулы и разрежается на другом; из-за этого возникает положительная сила на первом конце и равная ей отрицательная — на втором. Максвелл целиком принимает эту концепцию. В своем «Трактате» он пишет: «Электрическая поляризация диэлектрика представляет собой состояние деформации, в которое тело приходит под действием электродвижущей силы и которое исчезает одновременно с прекращением этой силы. Мы можем представить себе ее как нечто такое, что можно назвать электрическим смещением, производимым электродвижущей силой. Когда электродвижущая сила действует в проводящей среде, она вызывает там ток, но если среда непроводящая или диэлектрическая, то ток не может проходить через эту среду. Электричество, однако, смещено в ней в направлении действия электродвижущей силы, и величина этого смещения зависит от величины электродвижущей силы. Если электродвижущая сила увеличивается или уменьшается, то в той же пропорции соответственно увеличивается или уменьшается и электрическое смещение. Величина смещения измеряется количеством электричества, пересекающего единицу поверхности при возрастании смещения от нуля до максимальной величины. Такова, следовательно, мера электрической поляризации». Если поляризованный диэлектрик состоит из совокупности рассеянных в изолирующей среде проводящих частиц, на которых электричество распределено определенным образом, то всякое изменение состояния поляризации должно сопровождаться изменением распределения электричества в каждой частице, т. е. настоящим электрическим током, правда ограниченным лишь объемом проводящей частицы. Иначе говоря, каждое изменение состояния поляризации сопровождается током смещения. В том же «Трактате» Максвелл говорит: «Изменения электрического смещения, очевидно, вызывают электрические токи. Но эти токи могут существовать лишь во время изменения смещения, а поскольку смещение не может превысить некоторой величины, не вызывая разрушительного разряда, то эти токи не могут продолжаться бесконечно в одном и том же направлении, подобно токам в проводниках». После того как Максвелл вводит понятие напряженности поля, представляющее собой математическое истолкование фарадеевского понятия поля сил, он записывает математическое соотношение для упомянутых понятий электрического смещения и тока смещения. Он приходит к выводу, что так называемый заряд проводника является поверхностным зарядом окружающего диэлектрика, что энергия накапливается в диэлектрике в виде состояния напряжения, что движение электричества подчиняется тем же условиям, что и движение несжимаемой жидкости. Сам Максвелл так резюмирует свою теорию: «Энергия электризации сосредоточена в диэлектрической среде, будь то твердое тело, жидкость или газ, плотная среда, или разреженная, или же совершенно лишенная весомой материи, лишь бы она была в состоянии передавать электрическое действие. Энергия заключена в каждой точке среды в виде состояния деформации, называемого электрической поляризацией, величина которой зависит от электродвижущей силы, действующей в этой точке... В диэлектрических жидкостях электрическая поляризация сопровождается натяжением в направлении линий индукции и равным ему давлением по всем направлениям, перпендикулярным линиям индукции; величина этого натяжения или давления на единицу поверхности численно равна энергии в единице объема в данной точке».

Трудно более ясно выразить основную идею такого подхода, являющуюся идеей Фарадея: местом, в котором совершаются электрические явления, является среда. Как бы желая подчеркнуть, что это и есть главное в его трактате, Максвелл заканчивает его следующими словами: «Если мы примем эту среду в качестве гипотезы, я считаю, что она должна занимать выдающееся место в наших исследованиях и что нам следовала бы попытаться сконструировать рациональное представление о всех деталях: ее действия, что и было моей постоянной целью в этом трактате». Обосновав теорию диэлектриков, Максвелл переносит её понятия с необходимыми поправками на магнетизм и создаёт теорию электромагнитной индукции. Всё своё теоретическое построение он резюмирует в нескольких, ставших теперь уже знаменитыми уравнениях. Эти уравнения сильно отличаются от обычных уравнений механики — они определяют структуру электромагнитного поля. В то время как законы механики применимы к областям пространства, в которых присутствует материя, уравнения Максвелла применимы для всего пространства независимо от того, присутствуют или не присутствуют там тела или электрические заряды. Они определяют изменения поля, тогда как законы механики определяют изменения материальных частиц. Кроме того, ньютоновская механика отказалась от непрерывности действия в пространстве и времени, тогда как уравнения Максвелла устанавливают непрерывность явлений. Они связывают события, смежные в пространстве и во времени. Такое понимание поля абсолютно согласуется с идеей Фарадея, но находится в непреодолимом противоречии с двухвековой традицией. Поэтому нет ничего удивительного в том, что оно встретило сопротивление. Возражения, которые выдвигались против теории электричества Максвелла, были многочисленны и относились как к фундаментальным понятиям, положенным в основу теории, так и, может быть в еще большей степени, к той слишком свободной манере, которой Максвелл пользуется при выводе следствий из неё. Уравнения, сформированные Дж. Максвеллом на основе накопленных в середине XIX в. экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, можно даже сказать решающее влияние не только на все области физики, непосредственно связанные с электромагнетизмом, но и на многие возникшие впоследствии фундаментальные теории. Уравнения Дж. Максвелла описывают любые электромагнитные поля. Но этим их значение не исчерпывается. Они были одной из отправных точек при создании общей теории относительности Альберта Эйнштейна. Эйнштейн писал: «Со времени обоснования теоретической физики Ньютоном наибольшее изменение в её теоретических основах, другими словами, в нашем представлении о структуре реальности, было достигнуто благодаря исследованиям электромагнитных явлений Фарадеем и Максвеллом». Уравнения Максвелла вошли и в квантовую механику, положив начало квантовой электродинамике. До сих пор нет ни одного факта, ставящего под сомнение уравнения Максвелла. Причём, не только в мире привычных для нас размеров и скоростей, но и в квантовой механике, теории относительности, связывая наши представления о мире. Теория Максвелла была разработана методом последовательного теоретического и математического обобщения основных экспериментальных законов электрических и магнитных явлений: закона Кулона в обобщённой форме на основании теоремы Гаусса, закона полного тока и закона электромагнитной индукции. Данная теория, феноменологическая по своей природе, выявила единство и тесную взаимосвязь электрических и магнитных полей, не связывая при этом характер и специфику их взаимодействия с внутренними механизмами взаимодействия поля и вещества. В отличие от господствовавших на то время ошибочных взглядов основывавшихся на концепции дальнодействия и допускающих мгновенное распространение в пространстве взаимодействий между заряженными частицами и не учитывавших роль промежуточной среды – поля, теория Дж. Максвелла напротив, показала, что электромагнитные взаимодействия могут передаваться от одной точки пространства к другой посредством материального агента - электромагнитного поля с конечной скоростью, равной скорости света. В 1865 г. Дж. Максвелл теоретически показал, что электромагнитное поле в виде электромагнитных волн может распространяться в пространстве с конечной скоростью, равной скорости света в вакууме 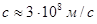. В общем случае под электромагнитным полем понимают форму материи, через которую осуществляется взаимодействие между электрически заряженными частицами. Понятие поля (электрического и магнитного) было введено в 1830 г. М. Фарадеем. Концепция поля стала возрождением теории близкодействия, основателем которой был Р. Декарт. В 60-х г.г. XIX в. развивая идеи М. Фарадея относительно природы электромагнитного поля, Дж. Максвелл раскрыл его природу и сформулировал основные законы. Согласно данных представлений заряженные частицы или токи образуют во всех точках окружающего пространства поле, действующее на другие заряженные частицы или токи, помещённые в произвольную точку этого пространства. Электромагнитное поле в вакууме характеризуется векторами напряжённости электрического поля 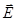и индукции магнитного поля 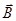. Этими векторами определяются силы, действующие со стороны электромагнитного поля на подвижные и неподвижные электрически заряженные частицы. В среде электромагнитное поле характеризуется двумя дополнительными параметрами: вектором смещения (индукции) электрического поля 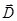и вектором напряжённости магнитного поля 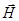. В теории Максвелла раскрывается электромагнитная природа света и таким образом собственно электрические и магнитные явления рассматриваются в совокупности и сведены воедино. Единство электрических и магнитных полей, наличие тесной взаимосвязи между ними позволили по-новому взглянуть на природу электромагнитных явлений и обобщить накопленные экспериментальные данные. Ещё М. Фарадей экспериментально выявил, что изменение во времени магнитного поля приводит к возникновению вихревого электрического поля (явление электромагнитной индукции). Из курса электродинамики известно, что источниками электрического поля могут быть либо электрические заряды, либо переменные во времени магнитные поля. В первом случае поле электрических зарядов описывается обобщённым на основании теоремы Гаусса законом Кулона, который можно представить дифференциальным уравнением вида:

учитывая, что:

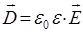
оно может быть преобразовано далее к виду:

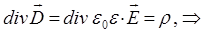
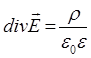
Последнее выражение представляет собой обобщённый закон Кулона, описывающий распределение зарядов в элементарном объёме вещества. Описываемое таким образом поле является потенциальным, циркуляция вектора напряжённости по произвольному замкнутому контуру равна нулю:

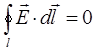
Силовые линии такого поля являются незамкнутыми: они выходят из позитивных зарядов (источников поля) или идут из бесконечности и входят в негативные заряды (стоки поля) или уходят в бесконечность. По этой причине электростатическое поле не может обеспечить непрерывное движение электрических зарядов вдоль замкнутых проводников, т.е. обеспечить направленное движение зарядов по замкнутому контуру. Для того чтобы в таком проводящем замкнутом контуре возникал и поддерживался длительное время электрический ток, необходимо наличие сторонних сил (сил неэлектрической природы), тогда очевидно:

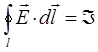
где - электродвижущая сила (ЭДС). Электрическое поле, которое возникает в контуре вследствие работы сторонних сил, существенно отличается от электростатического поля неподвижных зарядов. Линии напряжённости такого поля являются замкнутыми вдоль проводящего контура, по этой причине циркуляция такого вектора напряжённости будет принимать отличные от нуля значения, т.е.

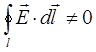
Электрические поля, возбуждаемые переменным магнитным полем являются вихревыми (соленоидальными). Для таких полей циркуляция вектора напряжённости по произвольному замкнутому контуру отлична от нуля и равна скорости изменения магнитного потока, пронизывающего произвольную поверхность, опирающуюся на контур интегрирования. Такие вихревые поля обуславливают непрерывное движение электрических зарядов вдоль замкнутых проводников, помещённых в это поле, т.е. приводят к возникновению индукционного тока. В основе электродинамики переменных полей лежит закон электромагнитной индукции, открытый в 1831 г. М Фарадеем, суть которого состоит в возникновении тока в произвольном замкнутом проводящем контуре при изменении магнитного потока, пронизывающего этот контур. Ещё в 1820 г. Х. Эрстед открыл, что вокруг проводников с током возникает магнитное поле. В том же году А. Ампер установил, что на проводники с током действует пондемоторная сила – механическая сила, не являющаяся по своей природе механической. Результаты этих исследований стали основой допущения, что электрическое поле можно получить за счёт магнитного. В 1831 г. М. Фарадей заметил, что электрические эффекты возникают только при изменении магнитного поля, т.е. при наложении переменного магнитного поля. Так, если в одном проводнике изменять электрический ток, то в соседнем также будет возникать электрический ток. К аналогичному результату можно прийти, если возле замкнутого проводника перемещать магнит. При этом электрический ток в обоих случаях будет наводиться (индуцироваться) переменным магнитным полем. Такой ток называют индукционным, а явление возникновения индукционного тока в проводнике под действием переменного магнитного поля - явлением электромагнитной индукции. Таким образом, открытие М. Фарадея состояло в том, что индукционный ток в замкнутом контуре может возникнуть во время движения проводящего контура в поле магнита, во время движения магнита относительно замкнутого контура, а также во время изменения тока в катушке, создающей магнитное поле. Всё это сводится к одному общему правилу: «Индукционный ток в замкнутом проводящем контуре возникает каждый раз при изменении магнитного потока пронизывающего замкнутый контур». Для того чтобы электрические заряды (электроны в проводнике) пришли в направленное движение, на них должны действовать сторонние силы , возникающие там, где имеет место изменение магнитного поля. Это в свою очередь привело к открытию закона, устанавливающего взаимосвязь между электрическим и магнитным полями. В тех областях, где имеет место изменение магнитного поля, возникает вихревое электрическое поле. Именно такое электрическое поле, возникающее в переменных магнитных полях, приводит к упорядоченному движению электронов в проводящем контуре, определяя, таким образом, возникновение ЭДС индукции при всяком изменении магнитного потока. Рассмотрим причину возникновения индукционного тока при наложении переменного магнитного поля. Так, в проводнике - проводящем замкнутом контуре, имеются позитивные заряды – ионы кристаллической решётки и свободные электроны проводимости – отрицательно заряженные ионы. При движении проводника в магнитном поле со скоростью 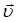, вместе с ним будут перемещаться также и заряды. При этом перемещение зарядов будет определять так называемый конвекционный ток. За направление электрического тока принимается движение положительных зарядов. Поскольку позитивные заряды связаны с кристаллической решёткой проводника и перемещаться не могут, то движущиеся электроны проводимости будут передавать своё движение ионам кристаллической решётки. В постоянном магнитном поле на движущиеся заряды будет действовать сила Лоренца, искривляющая траектории движения зарядов. Последняя направлена противоположно движению этих зарядов и в переменном магнитном поле создавать в проводнике индукционный ток, заряжая один конец проводника позитивно, а другой – негативно. Здесь сила Лоренца будет играть роль сторонних сил, т.е. поскольку по определению:

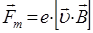
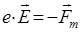
тогда соответственно:

Вследствие действия сторонних сил (силы Лоренца), проводник заряжается разноимённо, т.е. создаётся разность потенциалов, являющаяся причиной возникновения тока в замкнутом проводящем контуре. Эта разность потенциалов замыкает концы проводника, вследствие чего образовавшуюся систему можно считать замкнутым проводящим контуром. По определению, ЭДС определяется работой сторонних сил при перемещении единичного пробного заряда по замкнутому контуру. Если за замкнутый контур L взять контур произвольного проводника в переменном магнитном поле, тогда:

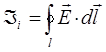
учитывая, что:

будем иметь соответственно:

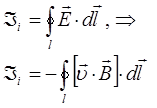
здесь 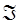- электродвижущая сила (ЭДС). Для того чтобы установить формулу для вычисления ЭДС индукции, удобно воспользоваться законом сохранения энергии. Впервые такие расчёты были проведены Г. Гельмгольцем. Так, на основании закона Ампера, имеем соответственно:

тогда под действием силы Ампера для одномерного случая (вдоль одной из координатных осей), работа:

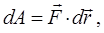
учитывая также выражение для элементарного потока магнитной индукции:

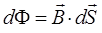
будем иметь соответственно:

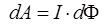
Если сопротивление проводящего контура равно 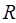, то согласно закону сохранения энергии, работа источника тока за время будет слагаться из работы нагревания проводника и работы перемещения его в магнитном поле. Поскольку по определению для ЭДС справедливо уравнение вида:

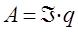
или переходя к бесконечно малым, имеем:

учитывая также, что:

приходим к выражениям вида:

тогда:

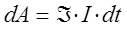
Полученное нами выше последнее уравнение представляет собой ту работу, которую выполняю сторонние силы (силы источника тока) за время . Для того чтобы вычислить работу идущую на нагревание проводника при прохождении через него тока силой , необходимо знать падение напряжения на данном участке проводника. Падение напряжения можно вычислить на основании уравнения вида:

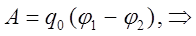
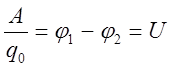
откуда следует, что:

или переходя к бесконечно малым величинам, будем иметь:

учитывая, что:

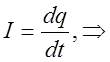
имеем:

На основании закона Ома для участка цепи:

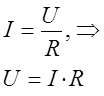
а также, что:

будем иметь соответственно:

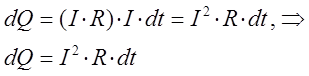
полученное уравнение:

представляет собой аналитическое выражение закона Джоуля – Ленца. Данное уравнение определяет работу, затрачиваемую на нагрев проводника сечением 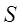при прохождении через него тока силой 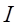. Таким образом, в ходе проделанных выше выкладок, приходим к выражениям для работы:

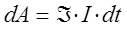
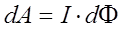
тогда соответственно будем иметь:

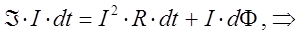
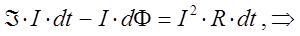
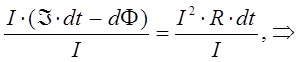
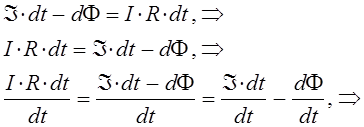
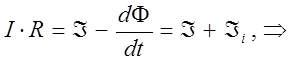
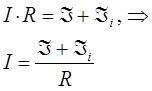
или для полной цепи:

здесь:

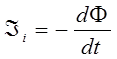
есть ЭДС индукции, которую можно определить как работу сторонних сил. Полученное таким образом уравнение представляет собой аналитическое выражение закона электромагнитной индукции: «ЭДС электромагнитной индукции 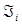в контуре, численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим замкнутым контуром».

Таким образом, в ходе проведения указанных выше преобразований, приходим соответственно к уравнениям вида:

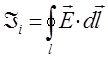
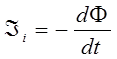
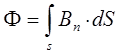
тогда соответственно будем иметь:

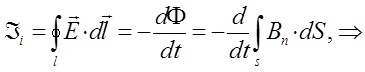
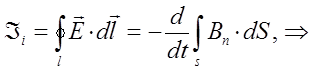
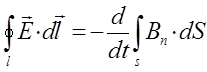
Полученное тождество также является выражением закона электромагнитной индукции М. Фарадея в интегральной форме (обобщённая запись): «При всяком изменении во времени потока магнитной индукции в точках пространства, где есть такое изменение, возбуждается вихревое электрическое поле, циркуляция напряжённости которого по произвольному замкнутому контуру L, равняется скорости изменения потока магнитной индукции сквозь замкнутую поверхность S, опирающуюся на этот контур L». Интересно отметить, что в отличие от потенциального электрического поля, циркуляция вектора, напряжённости которого по замкнутому контуру L равно нулю, т.е.

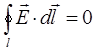
В отличие от потенциальных электростатических полей, электрическое поле возбуждаемое переменным магнитным полем будет вихревым, т.е. циркуляция вектора напряжённости по замкнутому контуру L будет отлична от нуля:

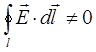
Действительно, на основании приведенных выше выкладок, не сложно заметить, что:

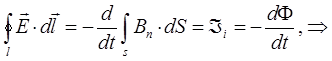
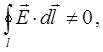
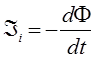
т.е. имеем:

Такое обобщение закона электромагнитной индукции было сделано впервые Дж. Максвеллом. Данное обобщение состояло в том, что он придал ему характер универсального закона, показав, что вихревое (соленоидальное) электрическое поле возникает везде, где имеет место переменное, изменяющееся во времени магнитное поле, независимо от того, имеется ли в этой области проводящий контур или его нет. Из закона электромагнитной индукции следует, что какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым контуром, возникающая в контуре ЭДС индукции всегда будет определяться выражением:

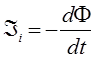
здесь знак минус показывает, что увеличение потока магнитной индукции:

будет вызывать уменьшение ЭДС индукции, а, следовательно, уменьшение работы сторонних сил в контуре, т.е.

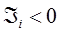
Это в свою очередь означает, что поле индукционного тока направлено навстречу потоку вектора магнитной индукции. Аналогично имеем:

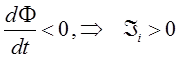
т.е. уменьшение потока магнитной индукции будет вызывать увеличение ЭДС индукции, что в свою очередь приведёт к увеличению работы сторонних сил, что приведёт к совпадению направлений поля индукционного тока и потока вектора магнитной индукции. Аналитическое выражение закона электромагнитной индукции М. Фарадея является обобщением правила Ленца для нахождения направления индукционного тока:

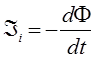
Согласно данному правилу «индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток» (правило Ленца). Полученное выше тождество вида:

на основании формулы Стокса:

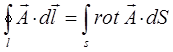
Может быть далее преобразовано далее к виду:

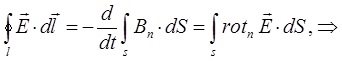
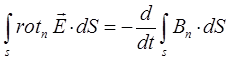
Поскольку контур интегрирования L и поверхность S, опирающаяся на него выбираются произвольно, тогда от равенства интегралов можно перейти к равенству соответствующих подынтегральных выражений:

учитывая, что направление на нормаль также является произвольным, а также что вектор магнитной индукции является функцией координат и времени (завися от них), тогда будем иметь соответственно:

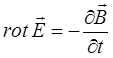
Полученное дифференциальное уравнение представляет собой закон электромагнитной индукции М. Фарадея, записанное в дифференциальной форме, обобщённый Дж. Максвеллом. Данное уравнение описывает закон возникновения вихревого электрического поля в определённой точке пространства, вследствие изменения индукции магнитного поля в этой точке и свидетельствует о том, что направление индукционного тока в замкнутом проводящем контуре зависит от характера изменения магнитного потока. Таким образом, в ходе проделанных выкладок было показано, что переменное магнитное поле порождает наведенное (индуцированное) электрическое поле. Если магнитное поле постоянно, то индуцированного электрического поля не возникает. Следовательно, индуцированное электрическое поле не связано с зарядами, как в случае электростатического поля; его силовые линии замкнуты, подобно силовым линиям магнитного поля. Это означает, что индуцированное электрическое поле, подобно магнитному, является вихревым. Если неподвижный проводник поместить в переменное магнитное поле, то в нём индуцируется ЭДС. При этом, как уже было показано выше, электроны приводятся в направленное движение электрическим полем и возникает индуцированный ток. В этом случае проводник является лишь индикатором индуцированного электрического поля. Поле приводит в движение свободные электроны в проводнике и тем самым обнаруживает себя. Теперь можно утверждать, что и без проводника это поле существует, обладая запасом энергии. Сущность явления электромагнитной индукции заключается не столько в появлении индуцированного тока, сколько в возникновении вихревого электрического поля. Это фундаментальное положение электродинамики установлено Максвеллом как обобщение закона электромагнитной индукции М. Фарадея. В отличие от электростатического поля, индуцированное электрическое поле является не потенциальным, так как работа, совершаемая в индуцированном электрическом поле при перемещении единичного положительного заряда по замкнутому контуру, равна ЭДС индукции, а не нулю. Направление вектора напряжённости вихревого электрического поля устанавливается в соответствии с законом электромагнитной индукции и правилом Ленца. На основании предложенной электромагнитной теории, Дж. Максвелл обобщил представления относительно электромагнитной индукции. Он показал, что возникновение индукционного тока в замкнутом контуре – частный случай вихревого электрического поля, возникающего в переменном магнитном поле. Так, М. Фарадей представлял электромагнитную индукцию как возбуждение электрического тока в замкнутом контуре под действием переменного магнитного поля. Дж. Максвелл показал, что суть явления электромагнитной индукции сводится к возникновению вихревого электрического поля во всех точках пространства, где есть переменное магнитное поле и таким образом для проявления электромагнитной индукции наличие проводника не обязательно. Таким образом, вихревое электрическое поле возникает везде, где есть переменное магнитное поле, силовые линии такого поля являются замкнутыми, оно способно индуцировать электрические токи. Обобщённый Дж. Максвеллом закон электромагнитной индукции определяется выражением вида:

Данное выражение показывает, что везде, где есть переменное магнитное поле, будет возникать вихревое электрическое поле. Таким образом, электромагнитное поле может существовать свободно, независимо от источников его образующих. Как уже говорилось ранее, электромагнитное поле в вакууме характеризуется векторами напряжённости электрического поля 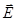и индукции магнитного поля 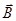. Этими векторами определяются силы, действующие со стороны электромагнитного поля на подвижные и неподвижные электрически заряженные частицы. В среде электромагнитное поле характеризуется двумя дополнительными параметрами: вектором смещения (индукции) электрического поля 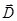и вектором напряжённости магнитного поля 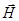. Соответствие между векторами напряжённости электрического поля 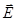и индукции магнитного поля 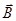, позволили предположить Дж. Максвеллу, что подобно уравнению, связывающему вектора 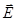и 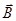, должно существовать уравнение, связывающее соответствующие друг другу вектора 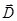и 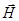, тогда:

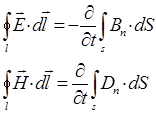
Действительно, с изменением во времени смещения (индукции) электрического поля возникает магнитодвижущая сила (МДС), что и предвидел Максвелл, т.е. имеем соответственно:

Вихревое магнитное поле создаётся также токами проводимости (закон полного тока):

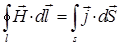
учитывая, что:

тогда соответственно будем иметь:

Из полученного равенства следует, что в природе существуют два источника вихревого магнитного поля - токи проводимости и переменное электрическое поле, определяемые членами вида:

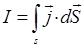
Поскольку переменное во времени электрическое поле создаёт вихревое магнитное поле также само, как и токи проводимости, тогда:

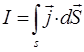
тогда на основании формулы Стокса:

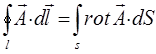
выражение:

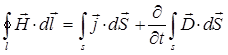
можно представить к виду:

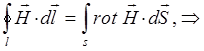
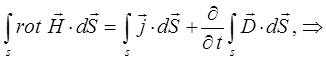
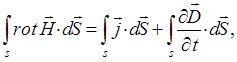
Поскольку интегрирование ведётся по произвольному контуру и поверхностям, тогда от равенства интегралов можно перейти к равенству соответствующих подынтегральных выражений:

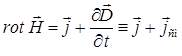
Из полученного выражения, очевидно, что вихревое магнитное поле образуется током проводимости 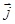и током смещения 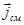, т.е.

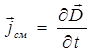
поскольку по определению:

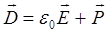
здесь первый член представляет собой чистый ток смещения, второй –поляризационный ток смещения. Поляризационный ток смешения связан со смещением под действием электрического поля связанных зарядов и имеет некоторую аналогию с током проводимости. Чистый ток смещения 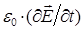никаких аналогов не имеет (отсутствие смещения зарядов), общего с током имеет только то, что одинаковым образом происходит возбуждение магнитного поля. В ходе проделанных выкладок, приходим к системе уравнений (в интегральной и дифференциальной формах), которые вместе с так называемыми материальными уравнениями составляют полную замкнутую систему уравнений:

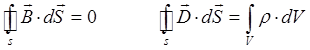
и в дифференциальной форме:

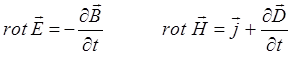
к материальным относят уравнения:

Первое уравнение Максвелла представляет собой аналитическое выражение закона электромагнитной индукции Фарадея. Обобщённый его физический смысл состоит в том, что всякое изменение во времени магнитного поля (переменное магнитное поле) возбуждает вихревое электрическое поле.

Второе уравнение Максвелла есть обобщённый закон Био-Саварра-Лапласа и является более общей формой закона полного тока, отражающего тот факт, что источниками вихревого магнитного поля могут быть токи проводимости и токи смещения (переменное электрическое поле).

Третье уравнение Максвелла указывает на отсутствие источников и стоков магнитного поля, подобных электрическому полю.

Четвёртое уравнение Максвелла является обобщением на основе теоремы Гаусса закона Кулона и физически указывает на существование в природе источников электрического поля в виде электрических зарядов, распределённых в пространстве с объёмной плотностью 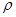. Уравнения Максвелла вместе с материальными уравнениями составляют полную замкнутую систему уравнений, позволяющую решить любую задачу макроскопической электродинамики. Так, для стационарных полей оказывается справедливым равенство вида:

и система уравнений Максвелла распадается на две независимые системы: на систему уравнений электростатического поля:

и систему уравнений магнитостатического поля:

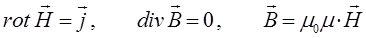
Таким образом, как это очевидно из приведенных выше рассуждений, статические электрические и магнитные поля не зависят друг от друга. При этом источниками электрических полей будут являться электрические заряды, а источниками магнитных полей – токи проводимости. Для вакуума, уравнения Максвелла для электрического и магнитного полей становятся симметричными. При этом материальные уравнения:

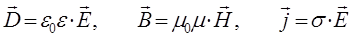
и собственно уравнения Максвелла:

в соответствии с указанными выше условиями для случая вакуума ( 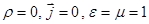), могут быть преобразованы и представлены к виду:

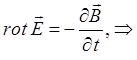
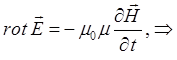
Аналогично используя материальные уравнения и соответствующие граничные, физически осмысленные условия для случая вакуума, преобразовываем второе уравнение Максвелла к виду:

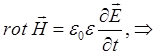
учитывая, что:

,

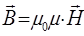дифференциальное уравнение:

может быть преобразовано к виду:

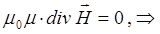
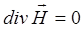
и аналогично, с учётом того, что:

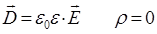
дифференциальное уравнение:

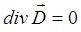
может быть представлено далее к виду:

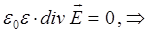
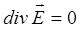
Таким образом, для случая вакуума, система уравнений Максвелла может быть представлена уравнениями вида:

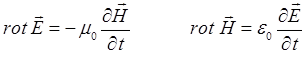
очевидно, здесь источниками вихревого магнитного поля будут переменные электрические поля, а источниками вихревого электрического поля - переменные магнитные поля. Рассмотрим теперь электромагнитное поле в однородном изотропном диэлектрике ( 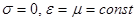), в котором отсутствуют свободные электрические заряды ( ). При этом материальные уравнения и собственно уравнения Максвелла, которые при данных условиях:

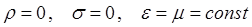
могут быть в таком случае представлены к виду, определяющему взаимосвязь электрического и магнитного полей. Имеем соответственно:

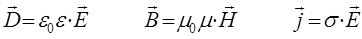
а также:

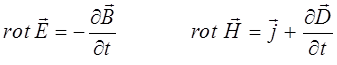
Тогда в соответствии с указанными выше физически осмысленными условиями, первое уравнение Максвелла может быть записано в виде:

из второго уравнения Максвелла:

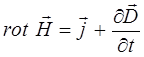
и условий вида:

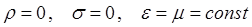
а также с учётом материальных уравнений:

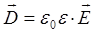
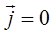
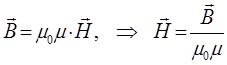
будем иметь соответственно:

В соответствии с указанными выше условиями:

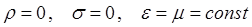
а также с учётом материальных уравнений:

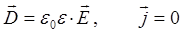
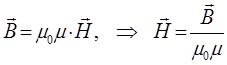
два других уравнения Максвелла могут быть переписаны в виде:

и таким образом, для описания электромагнитного поля в диэлектрике приходим к системе дифференциальных уравнений вида:

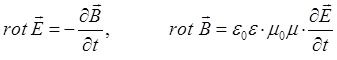
Полученные уравнения показывают, что электромагнитные волны, распространяются в пространстве с конечной скоростью самостоятельно, не зависимо от источников электромагнитного поля. Действительно, из полученных выше уравнений следует, что любое изменение во времени электрического поля 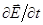приводит к возникновению в пространстве вихревого магнитного поля 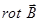и, в свою очередь, переменное магнитное поле 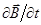приводит к возникновению вихревого электрического поля . Переменные электрическое и магнитное поля едины и взаимно обуславливают друг друга, образуя, таким образом, особую форму материи – электромагнитное поле, которое возникнув в определённых точках пространства, не заполняет его мгновенно, а распространяется в виде электромагнитных колебаний, с конечной скоростью, значения которой зависит от свойств среды, в которой распространяются электромагнитные колебания. Полученные выше уравнения можно свести к волновым дифференциальным уравнениям, решением которых являются уравнения волны. Для их получения, продифференцируем обе части уравнения:

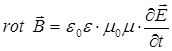
по времени, и учтём независимость операций дифференцирования по времени и координатам, поскольку среда, в которой распространяются электромагнитные колебания, считается неподвижной, и таким образом будем иметь соответственно:

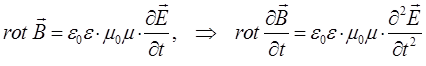
учитывая, что:

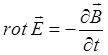
имеем:

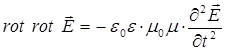
В векторном анализе широко используются так называемые векторные операции первого порядка и дифференциальные операции второго порядка:

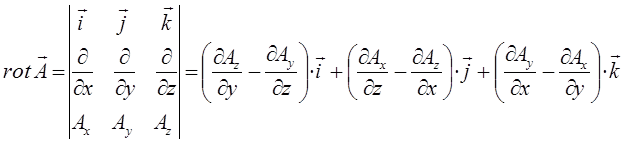
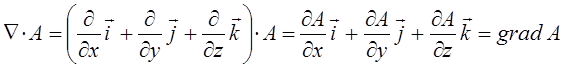
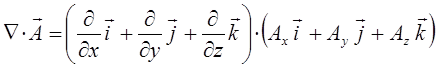
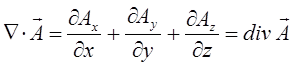
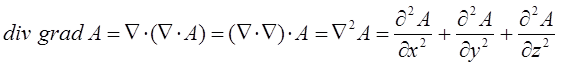
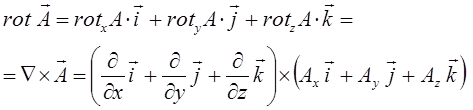
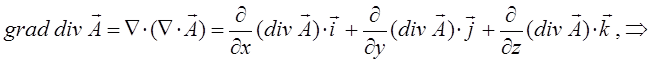
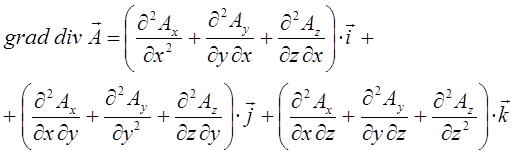
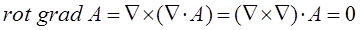
Так как векторное произведение двух одинаковых векторов равно нулю (получается нуль-вектор). Это означает, что поле градиента есть поле без вихревое (потенциальное).

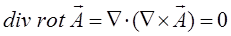
Так как смешанное произведение трёх векторов, два из которых одинаковы, дают нуль-вектор (равны нулю). Это означает, что поле вихря вектора – соленоидальное (трубчатое). В соленоидальном поле поток вектора через любую замкнутую поверхность равен нулю, т.е. поток, сохраняет своё постоянное значение и таким образом не имеет ни источников, ни стоков.

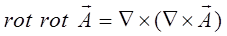
Для реализации данной дифференциальной операции, поступают как в случае смешанного произведения векторов:

тогда соответственно будем иметь:

итак, имеем:

тогда на основании приведенных выше выкладок, в соответствии с основными дифференциальными операциями второго порядка будем иметь соответственно:

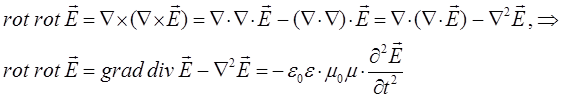
Учитывая, что 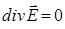, т.е. нет свободных зарядов, тогда соответственно:

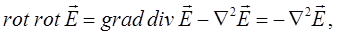
и таким образом имеем:

здесь:

Обобщая полученные результаты:

приходим к волновому уравнению вида:

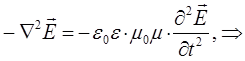
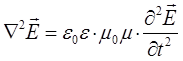
принимая отношение при условии и :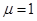

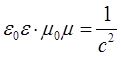
будем иметь соответственно для электрической составляющей электромагнитного излучения:

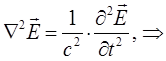
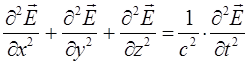
Проделав аналогичные операции для другого уравнения, будем иметь:

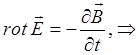
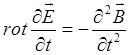
учитывая, что:

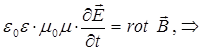
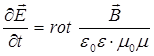
Подставив полученное выражение в исходное уравнение, будем иметь:

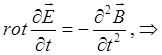
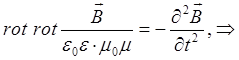
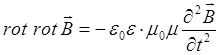
поскольку:

тогда соответственно для вектора магнитной индукции будем иметь:

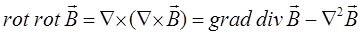
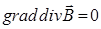Учитывая, что и как следствие , поэтому:

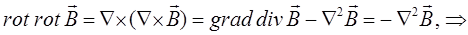
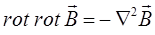
поскольку:

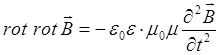
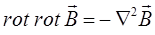
тогда соответственно:

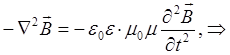
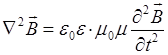
принимая отношение при условии и :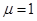

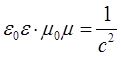
будем иметь соответственно для магнитной составляющей электромагнитного излучения выражение вида:

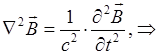
Таким образом, в ходе проделанных выкладок, приходим к двум выражениям для электрической и магнитной составляющих электромагнитного излучения:

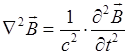
При выводе соответствующих волновых уравнений, мы формально ввели величину скорости:

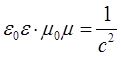
преобразуя данное уравнение, нетрудно показать, что данное соотношение справедливо, отвечает концепции близкодействия и для вакуума при условии и 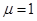, переходит в скорость света, т.е.

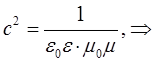
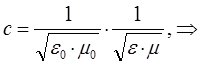
учитывая, что:

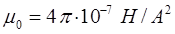
После подстановки значений данных постоянных в выражение для скорости 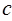, даёт:

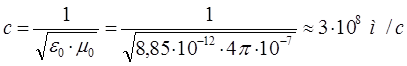
и таким образом для случая вакуума, значение формальной скорости света совпадают 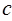, тогда полученные выше волновые уравнения для электрической и магнитной составляющих электромагнитной волны можно переписать в виде:

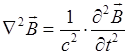
или

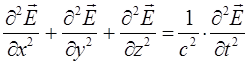
Интересно отметить, что при рассмотрении задачи на гармонический осциллятор, несложно получить уравнения волны:

распространяющейся в пространстве по закону синуса или косинуса, из которых после соответствующих преобразований можно легко получить волновое уравнение, описывающее распространение гармонических колебаний в пространстве:

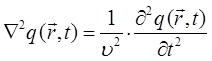
или в общем виде:

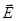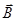При рассмотрении же электромагнитной теории Дж. Максвелла мы получили волновые уравнения, записанные через силовые характеристики электромагнитной волны и , аналогичные по физическому смыслу величине смещения. Очевидно, что уравнение плоской электромагнитной волны, распространяющейся в пространстве по закону синуса или косинуса по аналогии с механическими (упругими) волнами, можно будет также записать в виде:

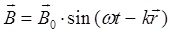
и соответственно:

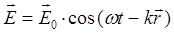
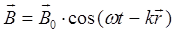
или в экспоненциальной форме:

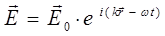
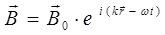
или

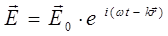
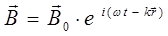
что хорошо видно из следующей схемы:

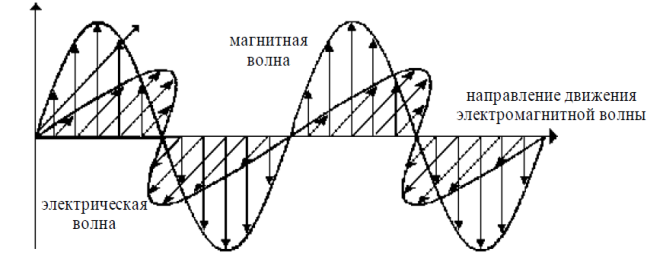
Рис. 1. Электромагнитная волна

Несоответствие нового содержания, появившегося в результате развития электромагнетизма, не только старой форме теории дальнодействия, но и механической теории эфира ощущал уже Фарадей, искавший для выражения этого содержания новую форму. Такую форму он усматривал в силовых линиях, которые следовало рассматривать не статически, а динамически. Развитию этой мысли посвящены его работы «Мысли о лучевых вибрациях» (1846) и «О физических линиях магнитной силы» (1851). Открытие Фарадеем в 1845 году связи между магнетизмом и светом явилось новым содержанием в учении о свете и вместе с тем еще раз указывало на строгую поперечность световых колебаний. Все это плохо укладывалось в старую форму механического эфира». Фарадей выдвигает идею силовых линий, в которых происходят поперечные колебания. «Нельзя ли, - пишет он, - предположить, что колебания, которые в известной теории (волновой теории света) принимаются за основу излучения и связанных с ним явлений, происходят в линиях сил, соединяющих частицы, а следовательно, массы материи в одно целое. Эта идея, если её допустить, освободит нас от эфира, являющегося с другой точки зрения той средой, в которой происходят эти колебания». Учёный указывает, что колебания, происходящие в линиях сил, представляют собой не механический процесс, а новую форму движения, «некий высший тип колебания». Подобные колебания поперечны и потому могут «объяснить чудесные разнообразные явления поляризации». Они не похожи на продольные звуковые волны в жидкостях и газах. Его теория, как он говорит, «пытается устранить эфир, но не колебания». Эти магнитные колебания распространяются с конечной скоростью: «...Появление изменения в одном конце силы заставляет предполагать последующее изменение на другом. Распространение света, а потому, вероятно, всех лучистых действий, требует времени, и чт