Затухающие колебания.
Любое реальное колебание происходит в какой-либо среде, которая оказывает сопротивление движению. На преодоление сопротивления среды расходуется часть энергии колеблющегося тела. Происходит рассеяние энергии и уменьшение амплитуды колебаний.
Колебания, амплитуда которых медленно уменьшается с течением времени, называются затухающими.
При достаточно малых скоростях сила сопротивления оказывается пропорциональной скорости:
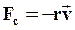 (23)
(23)
где r – коэффициент сопротивления, характеризующий взаимодействие тела со средой (r>0). Знак «-» показывает, что сила сопротивления направлена противоположно скорости.
II закон Ньютона при наличии сил сопротивления примет вид:
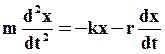 (24)
(24)
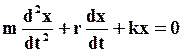
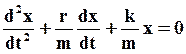
Ведем обозначения: 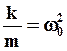 , где
, где 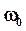 - частота собственных колебаний ГО;
- частота собственных колебаний ГО; 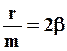 , где
, где  - коэффициент затухания. Тогда (24) перепишется в виде:
- коэффициент затухания. Тогда (24) перепишется в виде:
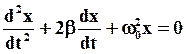 (25)
(25)
(25) – дифференциальное уравнение затухающих колебаний ГО.
Для решения этого уравнения введем новую переменную z, связанную с x соотношением:
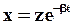 (26)
(26)
Найдем 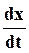 и
и 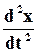 :
:


Подставим в (25) и вынесем 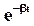 за скобки
за скобки
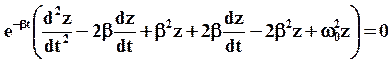
Разделим на 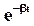 :
:
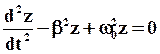
или:
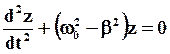 (27)
(27)
Предполагая, что сопротивление среды мало  , обозначим
, обозначим 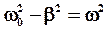 и запишем (27) в виде:
и запишем (27) в виде:
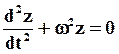 (28)
(28)
Его решение имеет вид:
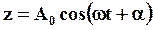 (29)
(29)
С учетом (26) получим уравнение затухающих колебаний:
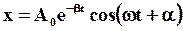 (30)
(30)
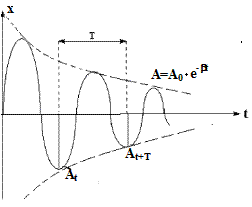
| Из (30) видно, что затухающие колебания можно рассматривать как гармонические колебания, амплитуда которых меняется по закону:
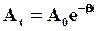 (31)
Циклическая частота затухающих колебаний: (31)
Циклическая частота затухающих колебаний:
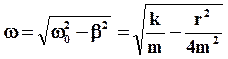 (32) (32)
|
период затухающих колебаний:
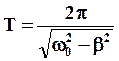 (33)
(33)
Выясним теперь физический смысл коэффициента затухания  .
.
Пусть 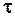 - промежуток времени, за который амплитуда колебаний уменьшилась в e раз.
- промежуток времени, за который амплитуда колебаний уменьшилась в e раз. 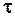 - время релаксации.
- время релаксации.
Найдем отношение амплитуд, соответствующих моментам времени t и (t+t):
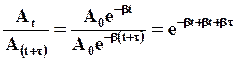 (34)
(34)
по определению t имеем  , откуда:
, откуда:
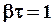 и
и  (35)
(35)
Следовательно, коэффициент затухания есть величина, обратная тому промежутку времени, за который амплитуда уменьшается в e раз.
Найдем теперь отношение двух амплитуд At и A(t+T), отстоящих друг от друга на период:
 (36)
(36)
Натуральный логарифм отношения двух амплитуд, отстоящих друг от друга на период, называется логарифмическим декрементом затухания:
 (37)
(37)
С учетом (36)
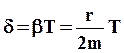 (38)
(38)
Обозначим через Ne – число колебаний, по истечении которых амплитуда уменьшается вe раз.
Тогда 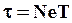 и
и 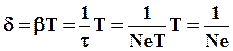 , т.е. логарифмический декремент затухания есть величина, обратная числу колебаний, по истечении которых амплитуда уменьшается в eраз.
, т.е. логарифмический декремент затухания есть величина, обратная числу колебаний, по истечении которых амплитуда уменьшается в eраз.
Для характеристики колебательной системы, кроме логарифмического декремента затухания, используется также величина:
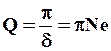 (39)
(39)
называемая добротностью контура.
Заметим, что все приведенные здесь вывода верны при 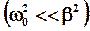 . Если затухание велико
. Если затухание велико 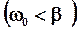 , то возникающее движение не является колебательным и носит апериодический характер.
, то возникающее движение не является колебательным и носит апериодический характер.
Дата добавления: 2014-12-09; просмотров: 1438;
