Собственные колебания гармонического осциллятора.
Рассмотри колебания частицы под действием упругой или квазиупругой силы 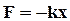 . Коэффициент
. Коэффициент  называется коэффициентом упругости. По второму закону Ньютона:
называется коэффициентом упругости. По второму закону Ньютона:
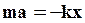
или 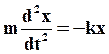 (5)
(5)
Разделим (5) почленно на массу частицы 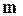 и обозначим:
и обозначим:
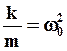 (6)
(6)
Тогда уравнение (5) примет вид:
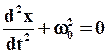 (7)
(7)
Решением дифференциального уравнения (7) являются функции:
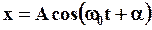 или
или
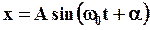 (8)
(8)
Таким образом, система, находящаяся под действием силы вида 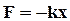 , совершает гармоническое колебание. Частота этого колебания:
, совершает гармоническое колебание. Частота этого колебания:
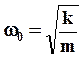 (9)
(9)
период колебания:
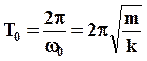 (10)
(10)
Дата добавления: 2014-12-09; просмотров: 1508;
