Кинематика гармонических колебаний.

Пусть закон движения гармонического осциллятора имеет вид:

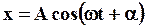
Выясним физический смысл входящих в него величин.

1. 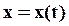характеризует изменение какой-либо физической величины при колебаниях, например, смещение маятника от положения равновесия, мгновенное значение заряда на конденсаторе в колебательном контуре, напряженности электрического поля в электромагнитной волне и т.д.

2. если 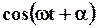примет максимальное значение, равное 1, то

Наибольшее отклонение гармонического осциллятора от положения равновесия называется амплитудой колебания.

3. Аргумент тригонометрической функции называется фазой колебания:

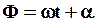
Фаза однозначно определяет значение колеблющейся величины в момент времени t.

4. При 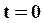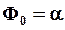называется начальной фазой колебания. Она однозначно определяет значение колеблющейся величины в начальный момент времени.

5. Время одного полного колебания называется периодом колебания .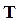

6. Число полных колебаний за единицу времени называется частотой колебания

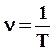
Эта единица называется Герцем (Гц)

7. Как известно, период косинуса равен 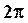, поэтому, полагая 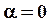, получим:

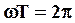, откуда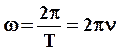

называется циклической или круговой частотой. Она равна числу колебаний за 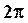секунд.

8.

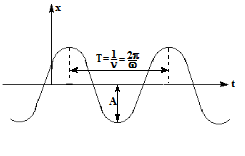
Графически гармоническое колебание можно представить в виде, представлено на рис:

9. Скорость 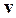и ускорение 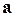при гармонических колебаниях равны соответственно:

(2)

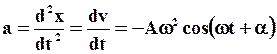(3)

10. Умножим (3) на массу осциллятора:

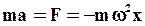(4)

Таким образом, гармонические колебания совершаются под действием силы, пропорциональной смещению и направленной в сторону, противоположную смещению.