Другие формы представления гармонических колебаний
а) Существует еще одна форма описания гармонических колебаний, в которой гармонические колебания описываются дифференциальным уравнением второго порядка.
Возьмем первую (скорость) и вторую (ускорение) производные по времени от величины 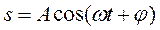 (11.1):
(11.1):
Скорость колеблющейся точки 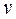 :
:
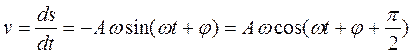 (11.6)
(11.6)
Ускорение колеблющейся точки 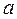 :
:
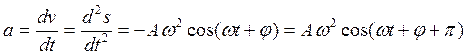 (11.7)
(11.7)
Получили также гармонические колебания скорости и ускорения с той же частотой 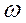 и амплитудами
и амплитудами 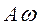 и
и 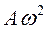 , соответственно. Фаза колебаний скорости
, соответственно. Фаза колебаний скорости 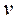 (11.6.) отличается от фазы колебаний смещения
(11.6.) отличается от фазы колебаний смещения 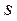 (11.1) на π/2, а фаза колебаний ускорения
(11.1) на π/2, а фаза колебаний ускорения 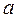 (11.7) отличается от от фазы колебаний смещения
(11.7) отличается от от фазы колебаний смещения 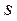 – на π.
– на π.
а) Дифференциальное уравнение гармонических колебаний.
Гармонический осциллятор
Из выражения (11.7) следует  , или
, или
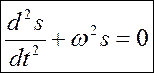 (11.8)
(11.8)
где 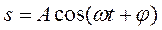 .
.
Это же выражение является решением этого уравнения.
ω –циклическая (круговая) частота,
t –время.
Колебательная система, описываемая уравнением вида (11.8) называется гармоническим осциллятором
б) Изображение гармонических колебаний
методом вращающегося вектора амплитуды или
методом векторных диаграмм
Гармонические колебания могут изображаться графически методом вращающегося вектора амплитуды или методом векторных диаграмм.Для этого из произвольной точки О, выбранной на оси x, под углом φ, равным начальной фазе колебаний, откладывается вектор А, модуль которого равен амплитуде рассматриваемого колебания (Рис. 11.2).
 Если этот вектор привести во вращение с угловой скоростью ω, равной циклической частоте колебаний, то проекция конца вектора будет перемещаться по оси x, принимая значения от +А до –А, а колеблющаяся величина s будет изменяться по закону
Если этот вектор привести во вращение с угловой скоростью ω, равной циклической частоте колебаний, то проекция конца вектора будет перемещаться по оси x, принимая значения от +А до –А, а колеблющаяся величина s будет изменяться по закону
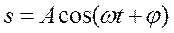
Т.обр., гармонические колебания можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды А, отложенного из произвольной точки оси под углом φ, вращающегося с угловой скоростью ω вокруг этой точки.
в) Представление гармонических колебаний комплексным числом
В физике часто применяется еще одна форма представления гармонических колебаний, в которой колеблющуюся величину представляют комплексным числом (Рис. 11.3). Согласно формуле Эйлера, для комплексных чисел справедлива запись:

|
Поэтому, полагая фазу 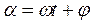 , уравнение гармонического колебания (11.1) можно записать в комплексной форме:
, уравнение гармонического колебания (11.1) можно записать в комплексной форме:
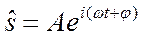 (11.10)
(11.10)
Вещественная часть (11.10):
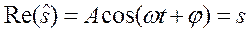
представляет собой гармоническое колебание.
Обозначение Re вещественной части будем опускать и (11.10) будем записывать в виде:
 (11.11)
(11.11)
В теории колебаний принимается, что колеблющаяся величина s равна вещественной части комплексного выражения (11.11).
Дата добавления: 2014-12-20; просмотров: 1945;

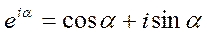 ,(11.9)
где
,(11.9)
где 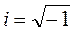 - мнимая единица.
- мнимая единица.
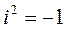
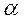 - фаза гармонического
колебания
- фаза гармонического
колебания