Параметры механических гармонических колебаний
Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси Х около положения равновесия, принятого за начало координат. Рассмотрим такие параметры, как смещение; скорость; ускорение; силу, действующую на м.т., а также механическую энергию колеблющейся материальной точки.
а) Смещение 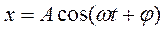 ,м (11.12)
,м (11.12)
б) Скорость:
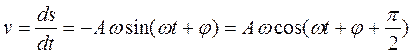 , м/с (11.13)
, м/с (11.13)
в) Ускорение: (11.14)
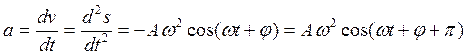 , м/с2
, м/с2
г) Сила, действующая на колеблющуюся материальную точку массой m равна:
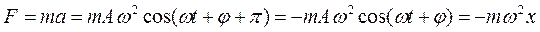
Таким образом, сила механических гармонических колебаний:
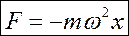 (11.15)
(11.15)
Эта сила действует на колеблющуюся материальную точку и называется восстанавливающей силой механических гармонических колебаний.
Она пропорциональна смещению материальной точки и направленав сторону, противоположную смещению (к положению равновесия).
Такая зависимость от смещения характерна для упругих сил и поэтому силы, которые аналогичным образом зависят от смещения, называются
квазиупругими.
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
е) Кинетическая энергия Т: (11.16)
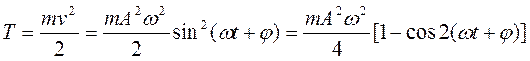
{ из тригонометрии: 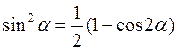 }
}
ж) Потенциальная энергия П: (11.17)
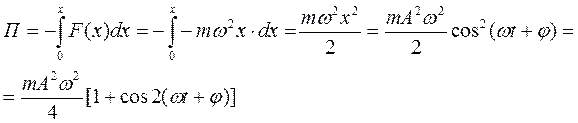
{ из тригонометрии: 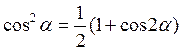 }
}
з) Полная энергия: сложив (11.16) и (11.17) получим формулу для полной механической энергии гармонически колеблющейся материальной точки.
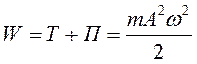 (11.18)
(11.18)
Очевидно, что полная энергия остается постоянной. С течением времени происходит только периодический переход кинетической энергии в потенциальную и обратно.
На Рис. 11.4. изображены временные диаграммы параметров гармонического колебательного процесса.
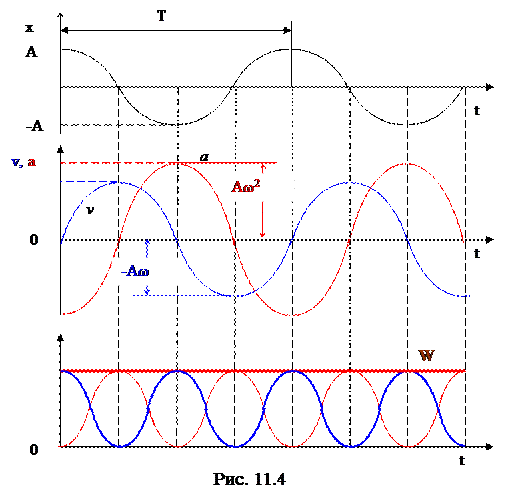
Полная энергия тела (материальной точки) остается постоянной, т.к. при гармонических колебаниях справедлив закон сохранения энергии, поскольку упругая сила консервативна.
Из формул для T и П следует, что кинетическая и потенциальная энергии изменяются по гармоническому закону с двойной частотой - 2ω.
На Рис. 11.4 представлены графики изменения параметров колебательного процесса.
Т.к. 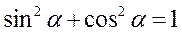 , то из формул (11.16 и 11.17) следует, что
, то из формул (11.16 и 11.17) следует, что
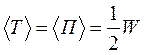 . (11.19)
. (11.19)
Из графиков видно, скорость точки максимальна при прохождении среднего положения.
Ускорение максимально в крайних положениях и всегда направлено к точке равновесия (где оно равно 0).
Амплитуды:
смещения 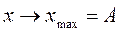 , м;
, м;
скорости 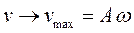 , м/с;
, м/с;
ускорения 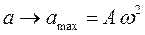 , м/с2.
, м/с2.
Из графиков (Рис. 11.3) видно, скорость точки максимальна при прохождении среднего положения.
Примерами гармонических колебаний являются пружинный, физический, математический маятники и электрический колебательный контур. Все эти примеры обобщаются колебательной системой, называемой гармоническим осциллятором.
Дата добавления: 2014-12-20; просмотров: 2230;
