Затухающие колебания. Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой.
Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой.
Система называется линейной, если ее параметры не меняются в ходе колебательного процесса. Линейные системы описываются линейными дифференциальными уравнениями.
а)Дифференциальное уравнение свободных
затухающих колебаний линейной системы
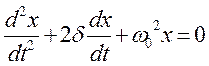(12.21)
где: x – колеблющаяся величина;
δ = const – коэффициент затухания;
ω0 – циклическая частота свободных незатухающих
колебаний (при δ = 0).
 |
В случае малых затуханий (δ2 << ω2) решение этого уравнения:
,
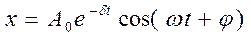где: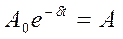 
–амплитуда затухающих колебаний.
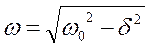– цикл. частота затухающих колебаний. (12.22)
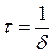- время релаксации – промежуток времени , (12.23)
в течение которого амплитуда затухающих колебаний уменьшается в е раз.
– Затухание нарушает периодичность колебаний.
– Затухающие колебания не являются периодическими.
Однако, если затухание мало, можно условно пользоваться понятием
периода затухающих колебаний:
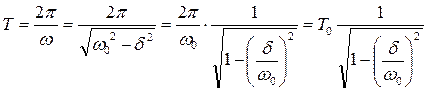
б)Декремент затухания
Если A(t) и A(t+T) – амплитуды двух последовательных колебаний, то их отношениеeδT– называется декрементом затухания:
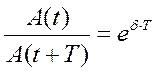(12.25)
{A(t+T) / A(t) = e-δT }
А натуральный логарифм этого отношения называется логарифмическим декрементом затухания:
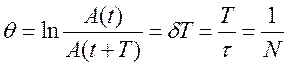(12.26)
Здесь N – число колебаний, совершаемых за время уменьшения амплитуды в е раз.
в) Добротность колебательной системы
Добротностью колебательной системы называется безразмерная величина Q, равная отношению энергии колебаний к ее убыли за один период, помноженному на 2π:
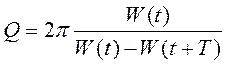(12.27)
Т.к. энергия колебаний W(t) пропорциональна квадрату амплитуды A2(t), то
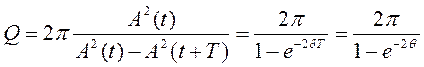(12.28)
При малых значениях логарифмического декремента затухания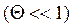 
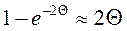, поэтому, принимая 
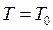добротность колеб.системы:
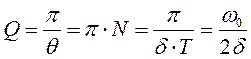( 1(12.29)2.29)
Дата добавления: 2014-12-20; просмотров: 1813;