ЗАДАНИЕ №11

Следующая задача контрольной работы такого типа :

Задана функция 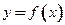. Установить, является ли данная функция непрерывной.

В случае разрыва функции в некоторой точке найти её пределы слева и справа,классифицировать характер разрыва. Построить схематично график функции.

Любая элементарная функция непрерывна во всех точках своей области определения.

Необходимое и достаточное условие непрерывности функции 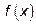в точке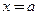

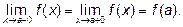
Скачок 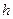функции 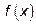в точке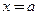

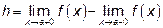
Пример 1.Пусть функция 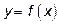имеет вид

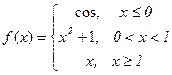
Решение: Функция 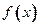определена для всех 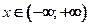. Если 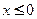, то ,

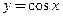поэтому для всех 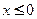функция непрерывна . Если 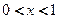, 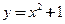непрерывна

для всех 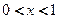.Если 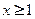, 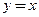для всех 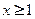также непрерывна .Поэтому точки разрыва

могут быть только для тех значений 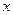, в которых заданная функция 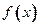меняет свой

аналитический вид, а именно в точках 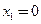и .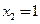

Исследуем непрерывность функции 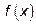в точке 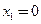. Для этого найдём:

предел слева

,

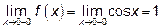предел справа

.

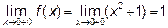
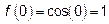Так как пределы слева и справа конечны, равны между собой и равны значению

функции 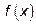в точке 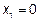, то получаем, что функция 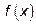непрерывна в точке .

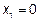Пусть 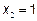. Находим аналогично

Предел слева

,

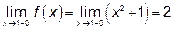Предел справа

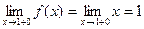
Так как пределы слева и справа конечны, но не равны между собой, то в точке

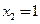функция имеет разрыв первого рода со скачком.

.

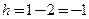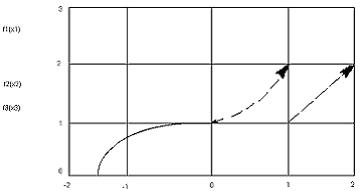
Строим график функции 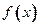, выделяя области определения составляющих

функций стрелками, если они не определены в точке 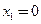или .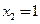

Подробнее об этом можно прочесть в [4] гл.2 §9, 10, 11, [1] гл.8 и задачи такого типа можно найти в [3] гл.6§6.