ЗАДАНИЕ №14
Следующая задача посвящена исследованию графика функции методами дифференциального исчисления.
Подробно об этом можно прочесть в [1], гл.11, [4] гл.5.
I.Методами дифференциального исчисления исследовать функцию 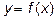 для
для 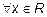 и по результатам исследования построить ее график.
и по результатам исследования построить ее график.
II.Найти наименьшее и наибольшее значения функции на отрезке[a;b].
I. Для исследования функции используется общая схема исследования функции.
- Найти область допустимых значений (ОДЗ) аргумента функции
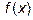 .
. - Найти точки пересечения функции
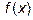 с осями координат Оx и Oy.
с осями координат Оx и Oy. - Найти точки разрыва и определить тип.
- Установить, является ли функция
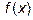 четной, нечетной и периодической.
четной, нечетной и периодической. - Найти асимптоты графика функции
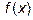 .
. - Найти
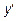 ,определить точки экстремумов
,определить точки экстремумов 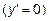 и интервалы возрастания
и интервалы возрастания 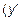 >0) и убывания
>0) и убывания 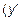 <0) графика функции
<0) графика функции 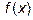 .
. - Найти
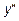 , определить точки перегиба (
, определить точки перегиба ( 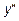 =0) и интервалы выпуклости (
=0) и интервалы выпуклости ( 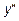 <0) и вогнутости (
<0) и вогнутости ( 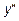 >0) графика функции
>0) графика функции 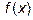 .
. - По результатам исследования построить график функции
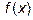 .
.
II. План нахождения наибольшего и наименьшего значений функции 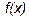 на отрезке [a,b].
на отрезке [a,b].
- Найти критические точки функции
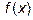
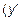 =0 или не существует).
=0 или не существует). - В каждой критической точке определить знак производной
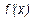 слева и справа. Если
слева и справа. Если 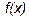 меняет знак при переходе через критическую точку, то в данной точке функция
меняет знак при переходе через критическую точку, то в данной точке функция 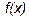 имеет локальный экстремум, иначе эта точка не является точкой экстремума.
имеет локальный экстремум, иначе эта точка не является точкой экстремума. - Вычислить значения функции
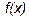 в точках экстремума и при x=a, x=b.
в точках экстремума и при x=a, x=b. - Среди этих значений найти наибольшее и наименьшее значения функции
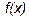 на отрезке [a,b].
на отрезке [a,b].
Пример 1.Пусть 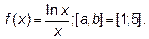 .
.
Решение:
- Функция
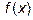 определена и непрерывна в интервале 0<x<+∞, т.к. область допустимых значений для функции y=lnx:
определена и непрерывна в интервале 0<x<+∞, т.к. область допустимых значений для функции y=lnx: 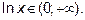
- В точке
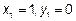 график
график 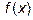 пересекает ось Ox. С осью Oy график функции
пересекает ось Ox. С осью Oy график функции 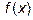 не пересекается.
не пересекается. - В граничной точке x=0 области допустимых значений функция
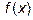 имеет бесконечный разрыв II рода, потому что
имеет бесконечный разрыв II рода, потому что

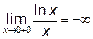 .
.
- Функция
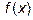 является четной, нечетной или периодической, если выполняется одно из равенств
является четной, нечетной или периодической, если выполняется одно из равенств 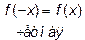 ,
, 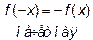 ,
, 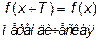 , где T>0 –период.
, где T>0 –период.
Заданная функция не является четной или нечетной, т.к. для x<0 она не определена.
Находим 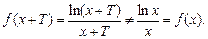
Следовательно, 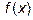 является функцией общего вида.
является функцией общего вида.
- Так как в точке x=0
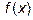 имеет бесконечный разрыв, то прямая x=0 (ось Oy) является вертикальной асимптотой.
имеет бесконечный разрыв, то прямая x=0 (ось Oy) является вертикальной асимптотой.
Ищем наклонные асимптоты 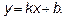 .
.
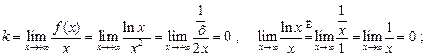
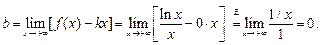
Поэтому 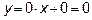 (ось Ox) есть горизонтальная асимптота (y=0)
(ось Ox) есть горизонтальная асимптота (y=0)
- Находим
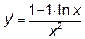 и критические точки:
и критические точки:
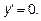

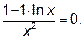 1-lnx=0. lnx=1. x=e.
1-lnx=0. lnx=1. x=e.
Исследуем знак производной в каждом из интервалов (O,e) и (e,∞), на которые критическая точка разбивает область определения функции.
Возьмем точку в (O,e), например, 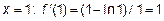 >0; возьмем точку в (e,∞), например,
>0; возьмем точку в (e,∞), например, 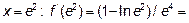
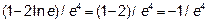 <0.
<0.
Составим таблицу
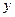
| (0,e) | e≈2.72 | (e,+∞) |
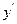
| + | - | |
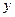
| Возрастает | 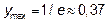
| Убывает |
- Находим вторую производную
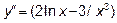 ,
, 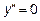 ,
, 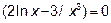 ,
, 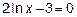 ,
, 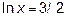 ,
, 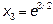 .
.
Определяем знак второй производной на интервалах 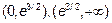 . Возьмем в интервале
. Возьмем в интервале 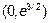 точку
точку 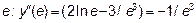 <0. Возьмем в интервале
<0. Возьмем в интервале 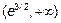 точку
точку 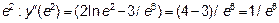 >0.
>0.
Составим таблицу
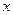
| 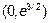
| 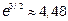
| 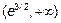
|
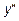
| - | + | |
| График | Выпуклый | 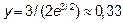
| Вогнутый |
Точка перегиба имеет координаты 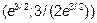 .
.
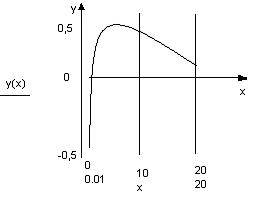
- На основании полученных данных строим график. По оси Ox удобно взять масштаб, равный 1, а по оси Oy, равный 0.1.
На отрезке [1; 5] функция имеет локальный максимум в точке 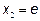 , равный
, равный 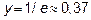 . Вычисляем значения функции
. Вычисляем значения функции 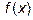 в точке x=1 и x=5: y(1)=0,
в точке x=1 и x=5: y(1)=0, 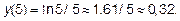 .
.
Следовательно, на отрезке [1; 5] 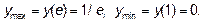 .
.
Решите самостоятельно следующие задачи:
14.1. Определите интервалы возрастания и убывания функции 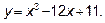 .
.
14.2. Найти экстремум функции 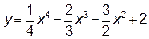 и определить ее наибольшее и наименьшее значение на отрезке [-2,4].
и определить ее наибольшее и наименьшее значение на отрезке [-2,4].
14.3. Найти асимптоты графика функции 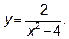 .
.
14.4. Найти асимптоты кривой 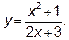 .
.
14.5. Исследовать функцию 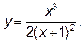 .
.
Задачи на эту тему можно найти в [3] гл.7 §2.
Дата добавления: 2014-12-09; просмотров: 683;
