ЗАДАНИЕ №13
Найти пределы функции, применяя правило Лопиталя.
Для раскрытия неопределённостей вида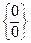 
или 
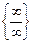используется правило Лопиталя:
Пусть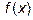 
и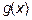 
две дифференцируемые на некотором интервале функции, причем 
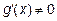, и пусть при 
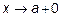(или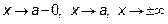 
), обе эти функции стремятся к нулю (или 
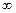). Тогда, если 
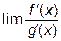при данном стремлении x существует, то существует и
.
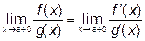Пример 1.Найти предел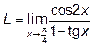 
Решение: При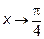 
имеем неопределённость 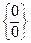. Функции 
, 
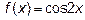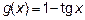, дифференцируемы в некоторой окрестности точки 
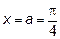, причем 
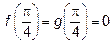. Если 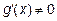, то по правилу Лопиталя получим:
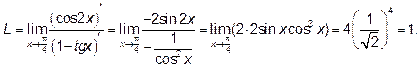
Ответ: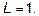 
Если отношение производных опять представляет собой неопределенность, вида 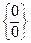или 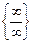, то можно снова применить правило Лопиталя, т.е. перейти к отношению вторых производных и т.д.
Пример 2.Найти предел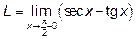
.
Решение: При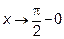 
получается неопределенность вида 
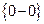. Выполняя преобразования, указанную неопределённость приведем к виду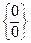
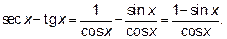
Теперь при 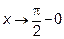и числитель, и знаменатель стремятся к нулю. Применяем правило Лопиталя
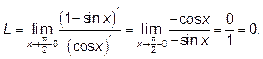
Ответ: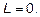 
Встречаются также неопределенности типа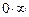 
. Они раскрываются аналогично предыдущему случаю, то есть приводятся к виду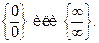 
Пример 3.Найти предел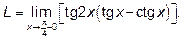
.
Решение : Здесь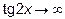 
, 
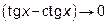при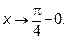 
. Следовательно имеем неопределенность 
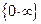. Приводим эту последовательность к виду 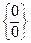и получаем
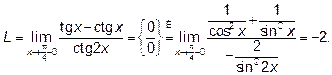
где буква Л над знаком равенства означает применение правила Лопиталя.
Ответ: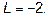 
Подробнее о вычислении пределов по правилу Лопиталя можно прочесть в [1] гл.4 §2, 4, 5 и найти соответствующие задачи в [3].
Следующие задачи решите самостоятельно:
13.1 Вычислить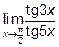 
13.2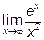 
13.3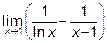 
Дата добавления: 2014-12-09; просмотров: 647;