ЗАДАНИЕ №16
Следующая задача посвящена вычислению определённого интеграла, например:
Пример 1.Вычислить определенный интеграл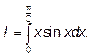 
Решение: Определенный интеграл от любой непрерывный функции f(x) вычисляется по формуле Ньютона-Лейбница
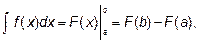
где F(x) – первообразная для f(x).
Геометрически определенный интеграл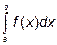 
представляет собой при 
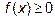площадь криволинейной трапеции, ограниченной кривой y=f(x), осью ox и прямыми x=a и x=b.
Проинтегрируем сначала соответствующий неопределенный интеграл по частям, положив u=x, dv=sin x dx.
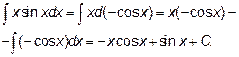
И по формуле Ньютона-Лейбница получим:
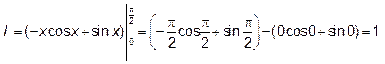
Пример 2.Найти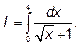 
Решение: Находя первообразную с помощью замены переменной при вычислении определенного интеграла, не следует забывать, что, изменив переменную, придется изменить и ее пределы интегрирования.
Обозначим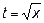 
, тогда 
, 
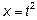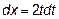, но при x=0, t=0, а при x=4, t=2. Следовательно, в новом интеграле, относительно переменной t изменяются пределы интегрирования:
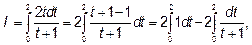
но так как dt=d(t+1)
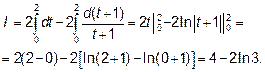
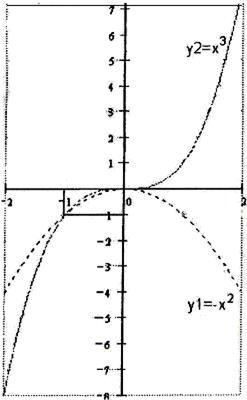
Пример 3. Найти площадь фигуры, ограниченной линиями: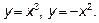 
Площадь фигуры типа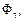 
для которой 
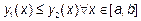, то есть, для правильной в направлении оси 
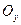фигуры на рисунке находятся по формуле
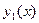
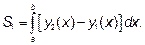
Для фигуры, правильной относительно оси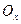 
на рисунке , то есть фигуры, которая ограничена
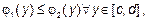
площадь находится по формуле
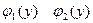
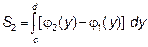
Решение: Решая совместно систему уравнений
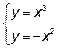
найдем абсциссы точек пересечения наших кривых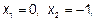 
следовательно, пределы интегрирования будут равны a=-1, b=0. Поскольку наша фигура является правильной, как относительно 
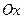, так и относительно 
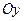, можно считать ее площадь по первой и по второй формуле. Будем считать по первой.
Тогда
Подробнее об определённых интегралах можно прочесть в [1] гл.XIII, [4] гл.11 и найти похожие задачи в [3] гл.10
Самостоятельно решите следующие задачи:
Вычислить:
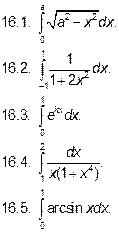
Дата добавления: 2014-12-09; просмотров: 615;